行 3.泊松分布实验 0.25 0.2 0.15 0.1 0.051 0 2 4 6 8 101214161820 12/60
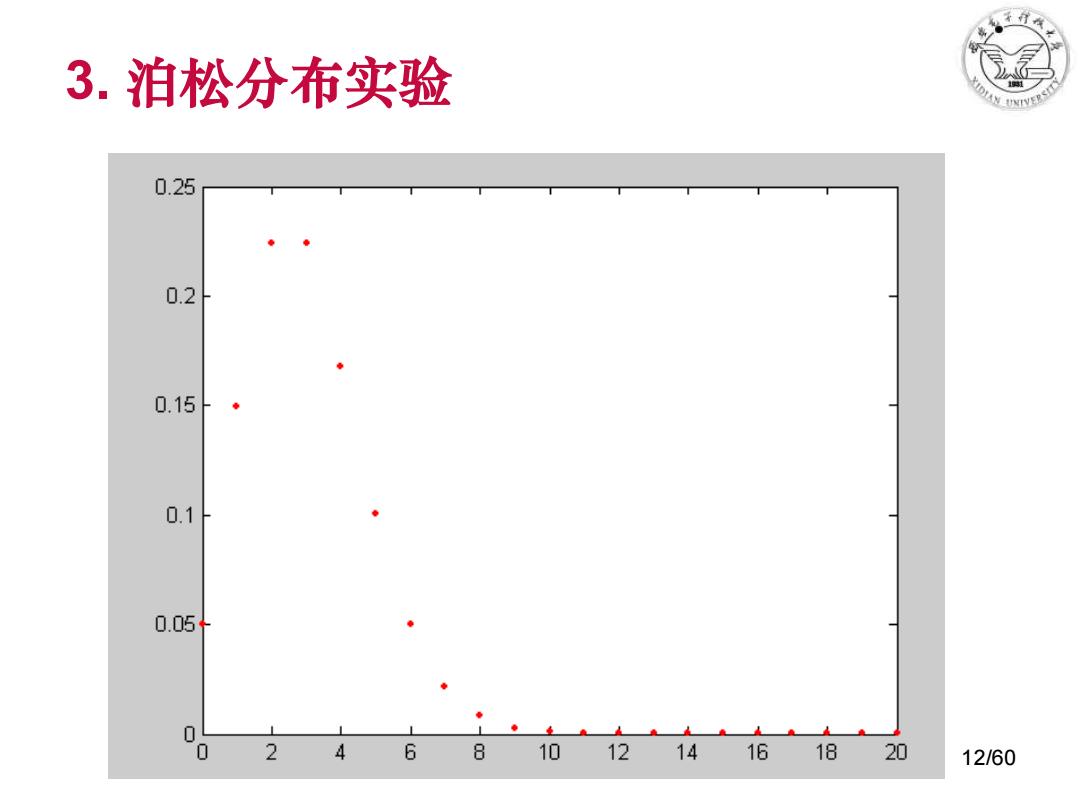
12/60 3. 泊松分布实验

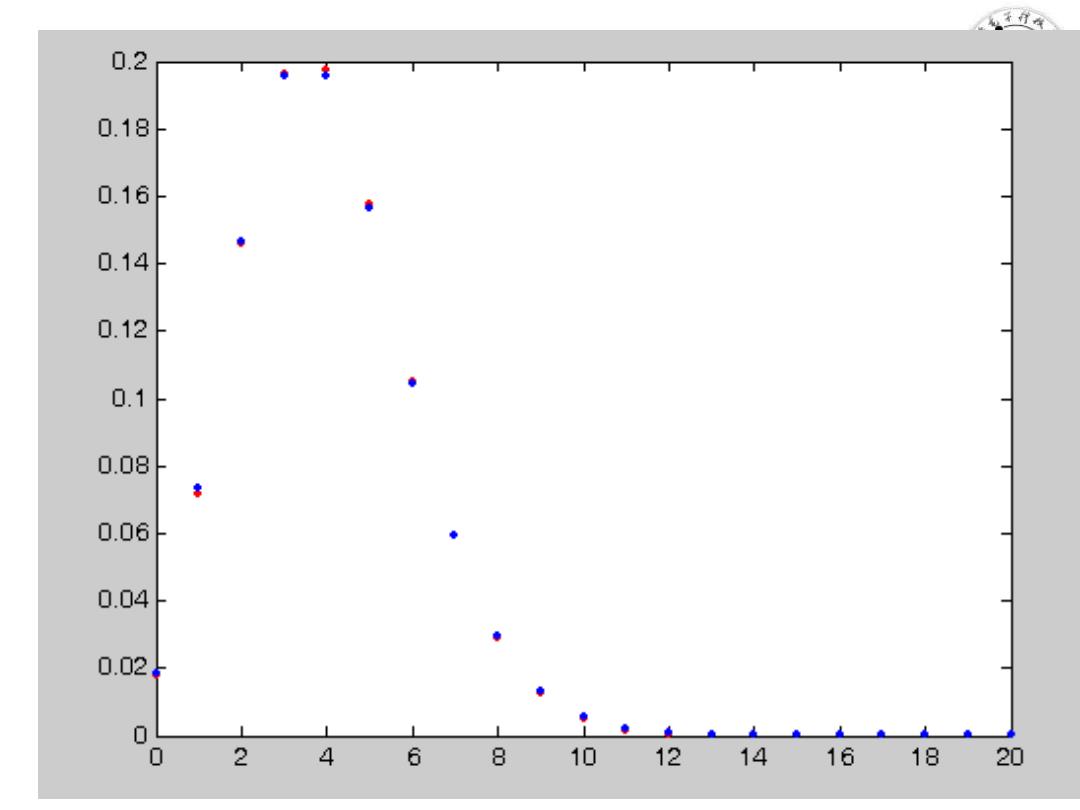
4.二项分布与泊松分布关系实验 。二项分布与泊松分布的关系 例7:X~b(200,0.02),Y服从参数为4的泊松 分布,划出分布率图像 ●x=0:20; ·y1=binopdf(x,200,0.02); ●y2=poisspdf(x,4); plot(x,yl,'r.',x,y2,'b.') 13/60
13/60 4. 二项分布与泊松分布关系实验 二项分布与泊松分布的关系 例7:X~b(200,0.02),Y 服从参数为4的泊松 分布,划出分布率图像 ⚫ x=0:20; ⚫ y1=binopdf(x,200,0.02); ⚫ y2=poisspdf(x,4); ⚫ plot(x,y1,’r.’,x,y2,’b.’)
0.2 0.18 0.16 0.14 0.12 0.1 0.08 0.06 0.04 0.02k 0 0 2 4 6 8 10 12141618 20
14/60

4.二项分布与泊松分布关系实验 9泊松定理 )(用泊松分布来逼近二项分布的定理) 设>0是一个常数,n是任意正整数,设吧m=2,则对于任意固定 的非负整数k,有 p-p,)=e 例9某种重大疾病的医疗险种,每份每年需交保险费100元,若在 这一年中,投保人得了这种疾病,则每份可以得到索赔额10000元, 假设该地区这种疾病的患病率为0.0002,现该险种共有10000份保 单,问: (1)保险公司亏本的概率是多少? (2)保险公司获利不少于80万元的概率是多少? 15/60
15/60 4. 二项分布与泊松分布关系实验 泊松定理 ⚫ (用泊松分布来逼近二项分布的定理) 设λ>0是一个常数,n是任意正整数,设npn =λ,则对于任意固定 的非负整数k,有 例9 某种重大疾病的医疗险种,每份每年需交保险费100元,若在 这一年中,投保人得了这种疾病,则每份可以得到索赔额10000元, 假设该地区这种疾病的患病率为0.0002,现该险种共有10000份保 单,问: (1)保险公司亏本的概率是多少? (2)保险公司获利不少于80万元的概率是多少? ! lim (1 ) k e p p k n k n k n k n n − − → − =

61 解设X表示这一年中发生索赔的份数,依题意,的统计规 律可用二项分布X~B10000,0.0002)来描述。由二项分布 与泊松分布的近似计算关系有 Cp'1-pt≈pem (0<p<10)) 9 X近似服从参数为2的泊松分布。 9 当索赔份数超过100份时,则保险公司发生亏本,亏本的 概率为 A=P61m=1-Mrs101-22e k=0 9 当索赔份数不超过20份时,则保险公司获利就不少于 80万元,其概率为p,=P(K<20)=之e k=0 I 16/60
16/60 解 设 表示这一年中发生索赔的份数,依题意, 的统计规 律可用二项分布 来描述。由二项分布 与泊松分布的近似计算关系有 近似服从参数为2的泊松分布。 当索赔份数超过100份时,则保险公司发生亏本,亏本的 概率为 当索赔份数不超过20份时,则保险公司获利就不少于 80万元,其概率为 X X X ~ B(10000,0.0002) ( ) ( ) (0 10) ! 1− − − e np k np C p p n p k k k n k n X ( ) ( ) = − = = − = − 100 0 2 1 ! 2 100 1 100 1 k k e k p P X P X ( ) = − = == 19 0 2 2 ! 2 20 k k e k p P X