
9>[p]=poisspdf([0:100],2);%计算101个泊松分布概率值 或[p]=binopdf([0:100],10000,0.0002);%按二项分布计算 9 p1=1-sum(p)%求出保险公司亏本的概率 p1=0.0000 9>[p]=poisspdf([0:19],2);%计算出20个泊松分布概率值 或[p]=binopdf([0:19],10000,0.0002);%按二项分布计算 9 p2=sum(p)%求出保险公司获利不少于80万元的概率 p2=1.0000 17/60
17/60 >> [p]=poisspdf([0:19],2);%计算出20个泊松分布概率值 或 [p]=binopdf([0:19],10000,0.0002); %按二项分布计算 p2=sum(p) %求出保险公司获利不少于80万元的概率 p2 = 1.0000 >> [p]=poisspdf([0:100],2);%计算101个泊松分布概率值 或 [p]=binopdf([0:100],10000,0.0002); %按二项分布计算 p1=1-sum(p) %求出保险公司亏本的概率 p1 = 0.0000
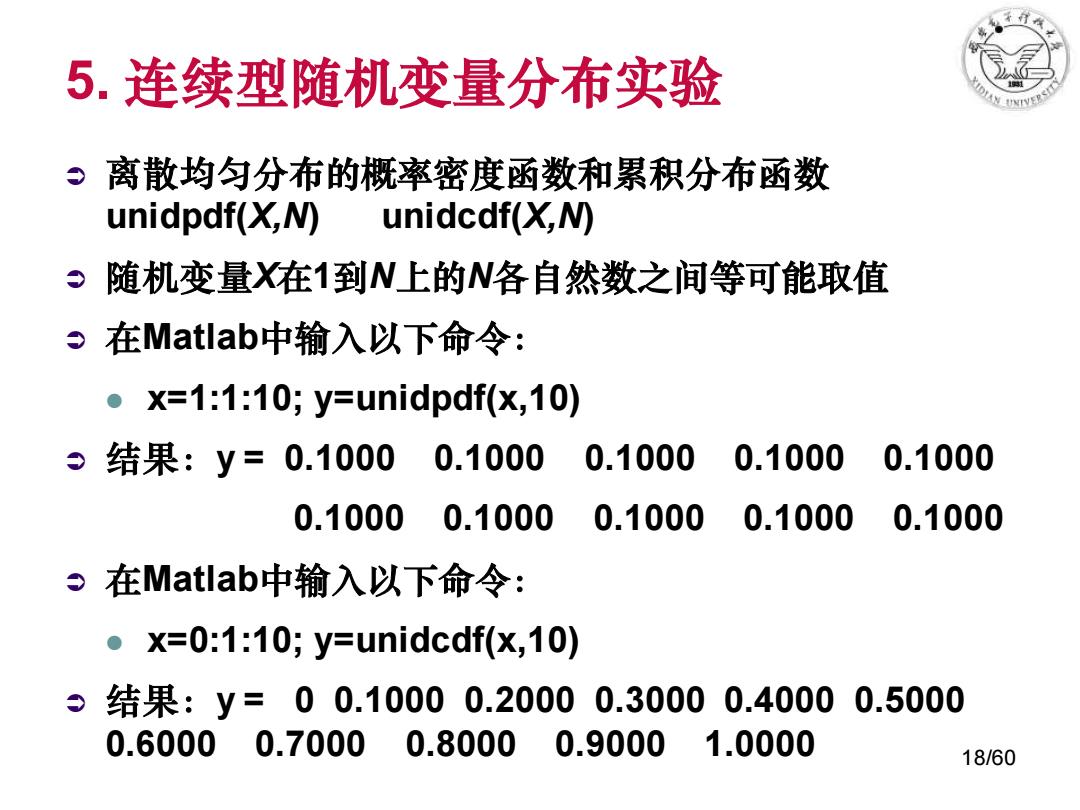
5.连续型随机变量分布实验 。离散均匀分布的概率密度函数和累积分布函数 unidpdf(X,N) unidcdf(X,N 随机变量X在1到N上的N各自然数之间等可能取值 在Matlab中输入以下命令: x=1:1:10;y=unidpdf(x,10) 9结果:y=0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 o在Matlab中输入以下命令: X=0:1:10;y=unidcdf(x,10) 9结果:y=00.10000.20000.30000.40000.5000 0.60000.7000 0.80000.9000 1.0000 18/60
18/60 5. 连续型随机变量分布实验 离散均匀分布的概率密度函数和累积分布函数 unidpdf(X,N) unidcdf(X,N) 随机变量X在1到N上的N各自然数之间等可能取值 在Matlab中输入以下命令: ⚫ x=1:1:10; y=unidpdf(x,10) 结果:y = 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 在Matlab中输入以下命令: ⚫ x=0:1:10; y=unidcdf(x,10) 结果:y = 0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000

5.连续型随机变量分布实验 。连续均匀分布 密度函数:f=unifpdf(x,a,b) 。分布函数:f=unifcdf(x,a,b) 例:画出均匀分布(2,5)的概率密度函数和分布函 数的图形. p在Matlab中输入以下命令: x=0:0.01:7; ●y=unifpdf(x,2,5); zunifcdf(x,2,5); plot(x,y,x,Z) 19/60
19/60 5. 连续型随机变量分布实验 连续均匀分布 ⚫ 密度函数:f=unifpdf(x,a,b) ⚫ 分布函数:f=unifcdf(x,a,b) 例: 画出均匀分布U(2,5)的概率密度函数和分布函 数的图形. 在Matlab中输入以下命令: ⚫ x=0:0.01:7; ⚫ y=unifpdf(x, 2, 5); ⚫ z=unifcdf(x, 2, 5); ⚫ plot(x,y,x,z)

1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 1 2 3 4 5 6 7 20/60
20/60

5.连续型随机变量分布实验 (2)指数分布 01 密度函数:fexppdf(x) 分布函数:F=expcdf(x,O) 。1 例:画出指数分布E()的概率密度函数和分布函数 的图形.求P(0<X<5)P(0<XK20) o在Matlab中输入以下命令: 0x=0:0.1:5; 0 y=exppdf(x,2); z=expcdf(x,2); plot(x,y,x,Z) result1=expcdf(5,2)-expcdf(0,2) result2=expcdf(20,2)-expcdf(0,2) 21/60
21/60 5. 连续型随机变量分布实验 (2) 指数分布 ⚫ 密度函数:f=exppdf(x,) ⚫ 分布函数:F=expcdf(x,) 例: 画出指数分布E(1)的概率密度函数和分布函数 的图形. 求P(0<X<5) P(0<X<20). 在Matlab中输入以下命令: ⚫ x=0:0.1:5; ⚫ y=exppdf(x,2); ⚫ z=expcdf(x,2); ⚫ plot(x,y,x,z) ⚫ result1=expcdf(5,2)-expcdf(0,2) ⚫ result2=expcdf(20,2)-expcdf(0,2)