例1计算由两条抛物线y2=x和y=x所围成的 图形的面积. =G3 1,2 1 x=y 解 两曲线的交点 0.8 0.6 (0,0)(1,1) 2 0.2 ◆ 选x为积分变量x∈[0,1] 0.20.4 0.60.8 湿 面积元素dA=(Wx-x2) 临-
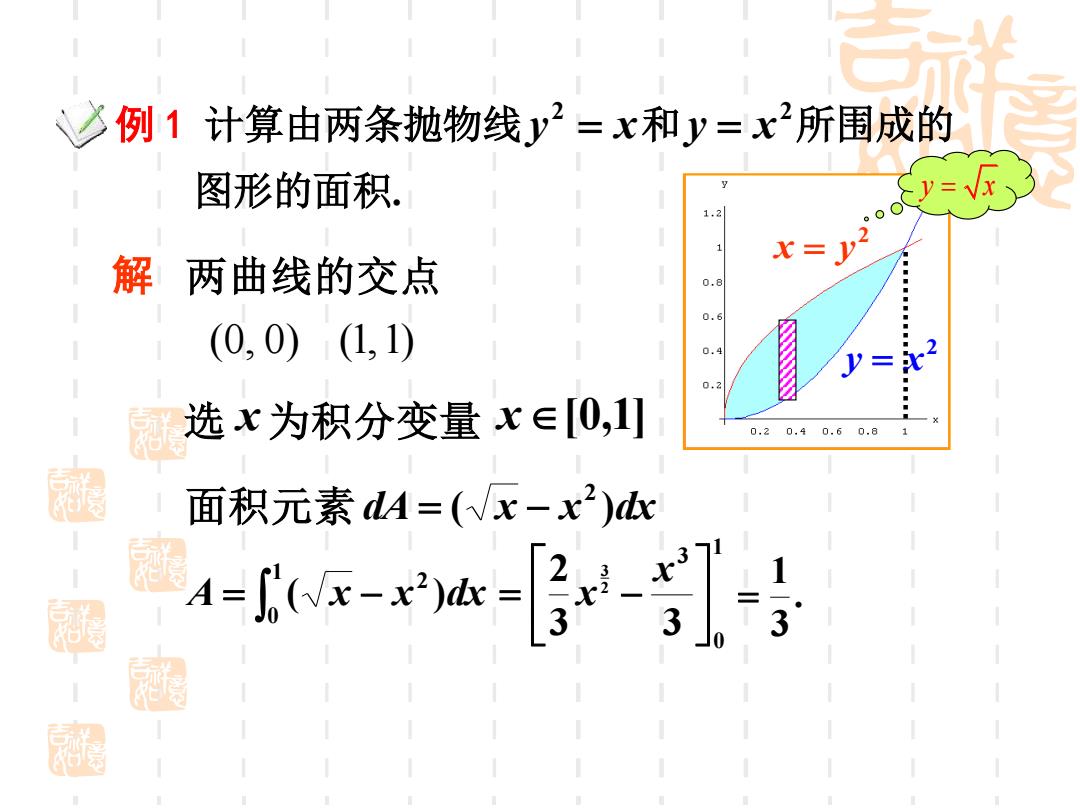
例 1 计算由两条抛物线 y = x 2 和 2 y = x 所围成的 图形的面积. 解 两曲线的交点 (0, 0) (1,1) 面积元素 dA ( x x )dx 2 = − 选 x 为积分变量 x[0,1] A ( x x )dx 2 1 0 = − 1 0 3 3 3 2 2 3 = − x x . 3 1 = 2 y = x 2 x = y y x =
少例2计算由曲线y2=2x和直线y=x-4所围 成的图形的面积. x=y+4 解两曲线的交点 V=x一4 [y2=2x y=x-4 =2X →(2,-2),(8,4) 湖 1选y为积分变量y∈[-2,4 4=+42)海=
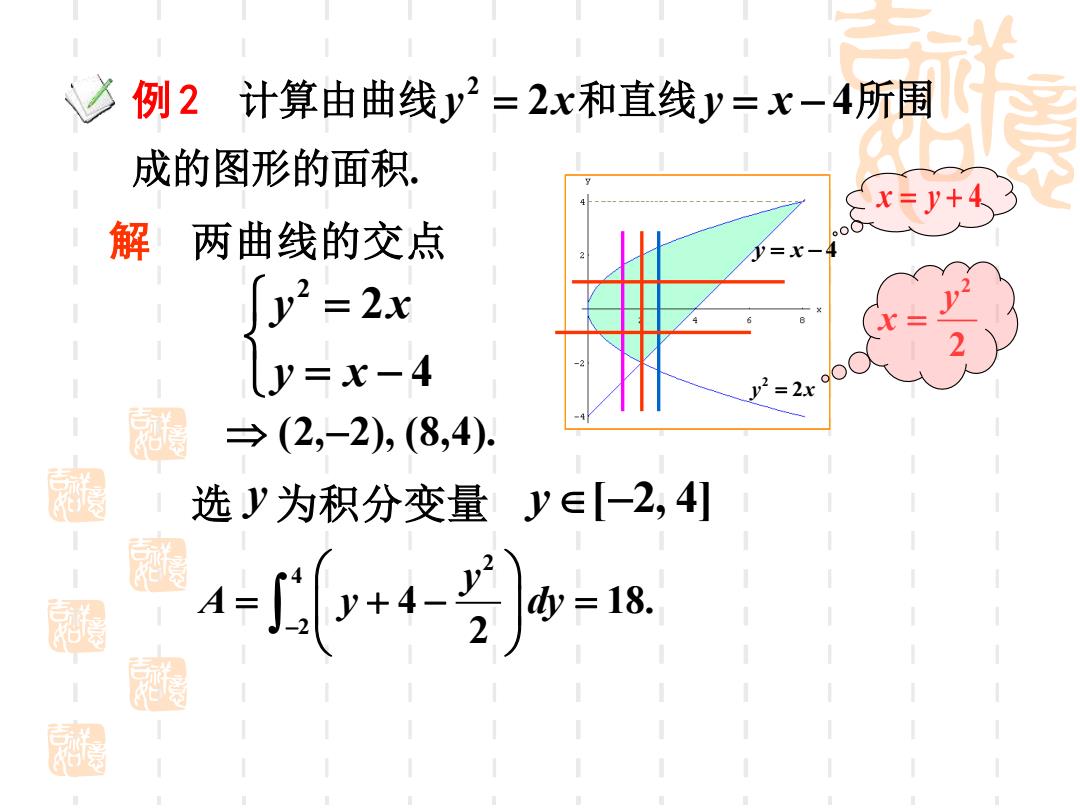
例 2 计算由曲线 y 2x 2 = 和直线y = x − 4所围 成的图形的面积. 解 两曲线的交点 (2,−2), (8,4). = − = 4 2 2 y x y x 选 y 为积分变量 y[−2, 4] 2 4 2 4 18. 2 y A y dy − = + − = y 2x 2 = y = x − 4 x y = + 4 2 2 y x =
2 少例3求椭圆 =1所围成的面积, 解 椭圆可看作直线x=一, x=M以及连续曲线 湿 所围成的平面图形,故 由面积公式可得椭圆面积为 dx
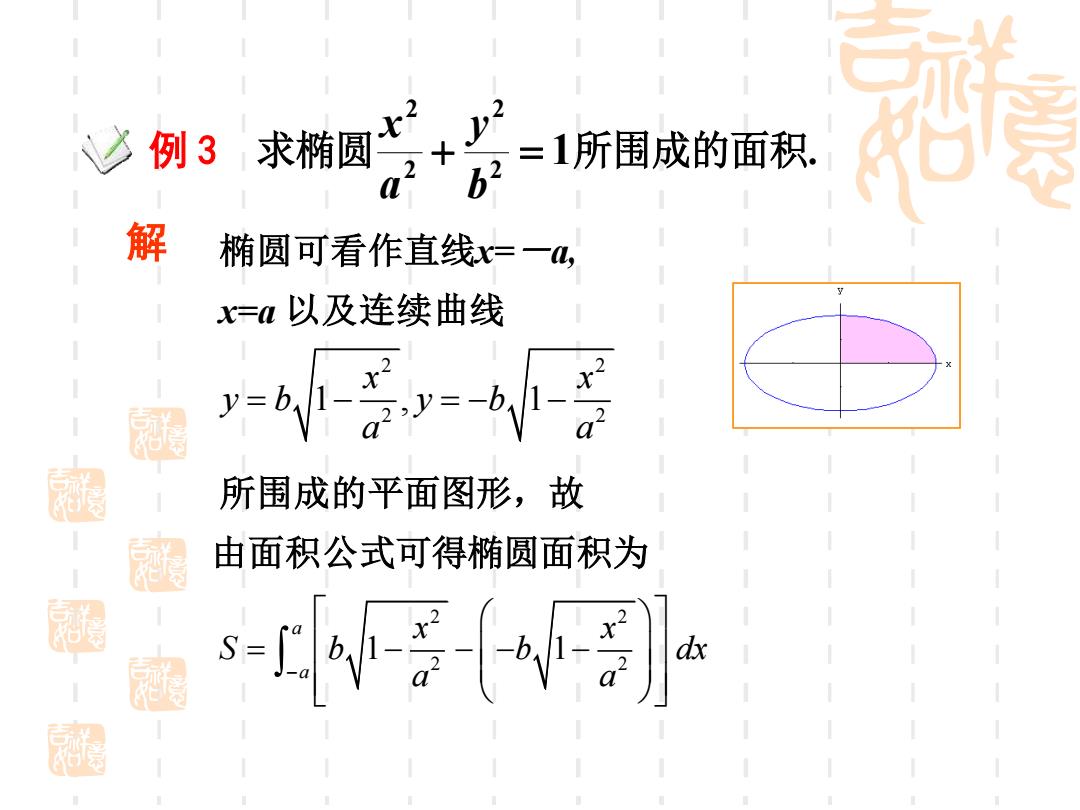
例 3 求椭圆 1 2 2 2 2 + = b y a x 所围成的面积. 解 椭圆可看作直线x=-a, x=a 以及连续曲线 2 2 2 2 1 , 1 x x y b y b a a = − = − − 所围成的平面图形,故 由面积公式可得椭圆面积为 2 2 2 2 1 1 a a x x S b b dx − a a = − − − −

-y2 d -2f6吾=46 dx costacostd 湿 π 4abj2 cos'd=πah 测 当a=b=R时,得到圆的面积公式S=πR #
2 2 2 1 a a x b dx − a = − 2 2 0 4 1 a x b dx a = − 2 0 4 cos cos b t a tdt = 2 2 0 4 cos ab tdt = = ab. 2 2 2 2 1 1 a a x x S b b dx − a a = − − − − 2 当a b R S R = = = 时,得到圆的面积公式 . #
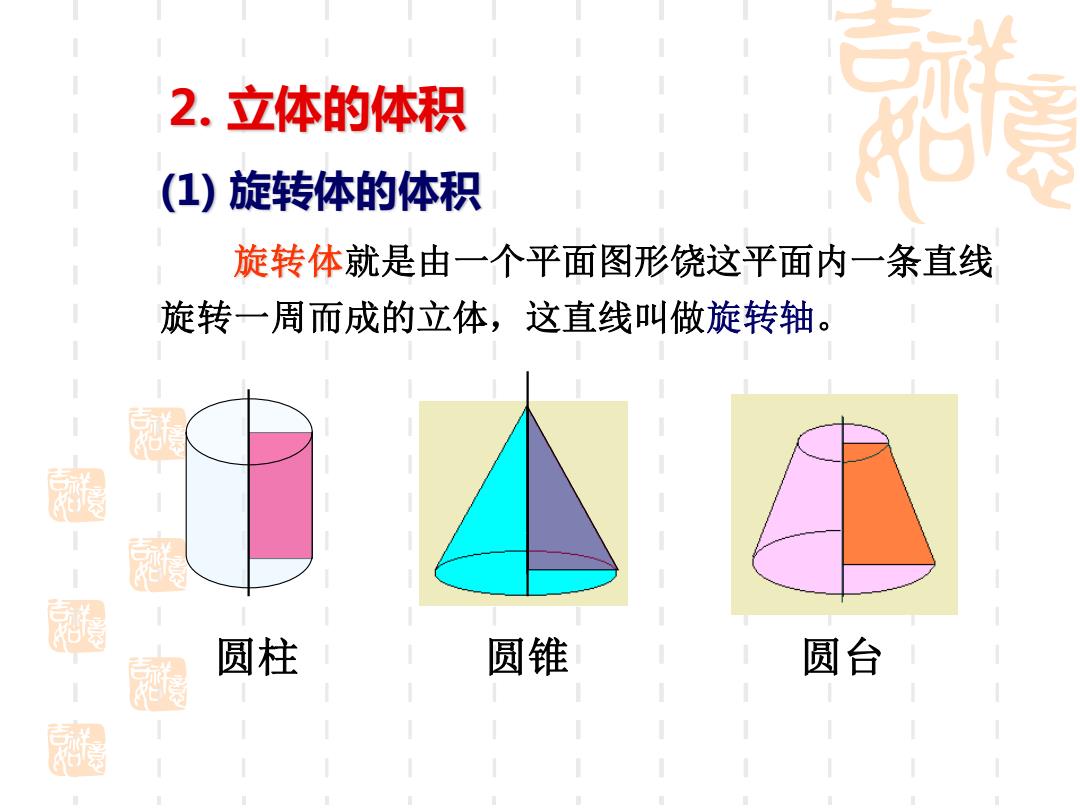
2.立体的体积 (1)旋转体的体积 旋转体就是由一个平面图形饶这平面内一条直线 旋转一周而成的立体,这直线叫做旋转轴。 圆柱 圆锥 圆台
旋转体就是由一个平面图形饶这平面内一条直线 旋转一周而成的立体,这直线叫做旋转轴。 圆柱 圆锥 圆台 (1) 旋转体的体积 2. 立体的体积