
第三章矩阵的运算 容易验证初等矩阵的逆矩阵仍然是同类的初等矩阵 E(i,j)1=E(i,j); E(k)=E(》 E(jk),)1=E((-k),). 对矩阵进行初等变换,可以用相应的初等矩阵左乘 或右乘矩阵来表示
第三章 矩阵的运算 1 1 1 ( , ) ( , ); 1 ( ( )) ( ( )); ( ( ), ) ( ( ), ) . E i j E i j E i k E i k E j k i E j k i − − − = = = − 容易验证初等矩阵的逆矩阵仍然是同类的初等矩阵 对矩阵进行初等变换,可以用相应的初等矩阵左乘 或右乘矩阵来表示

第三章矩阵的运算 例如 2 . an Nin A= 2 00 a mn
第三章 矩阵的运算 11 12 1 1 2 1 2 1 2 n i i in j j jn m m mn a a a a a a A a a a a a a = 例如
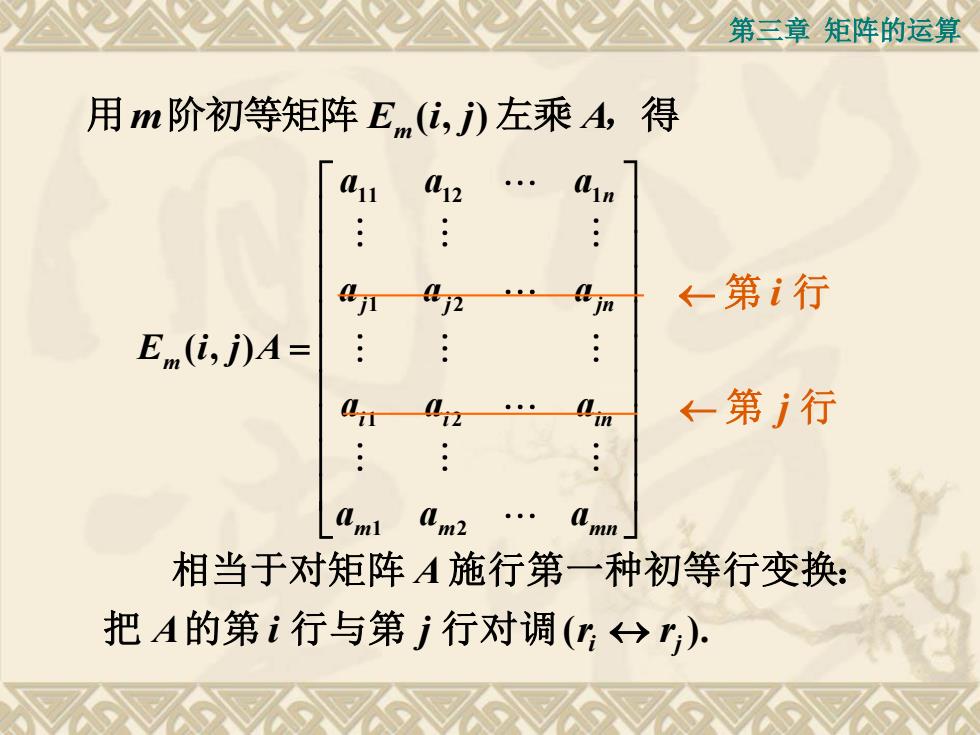
第三章矩阵的运算 用m阶初等矩阵E,m(i,)左乘A,得 12 m ←第i行 E(i,j)A= :: ←第j行 m2 mn 相当于对矩阵A施行第一种初等行变换: 把A的第i行与第j行对调(→)
第三章 矩阵的运算 ( , ) 用m E i j A 阶初等矩阵 m 左乘 ,得 11 12 1 1 2 1 2 1 2 ( , ) n j j jn m i i in m m mn a a a a a a E i j A a a a a a a = 第 i 行 第 j 行 ( ). i j A i j r r A 把 的第 行与第 行对调 相当于对矩阵 施行第一种初等行变换:
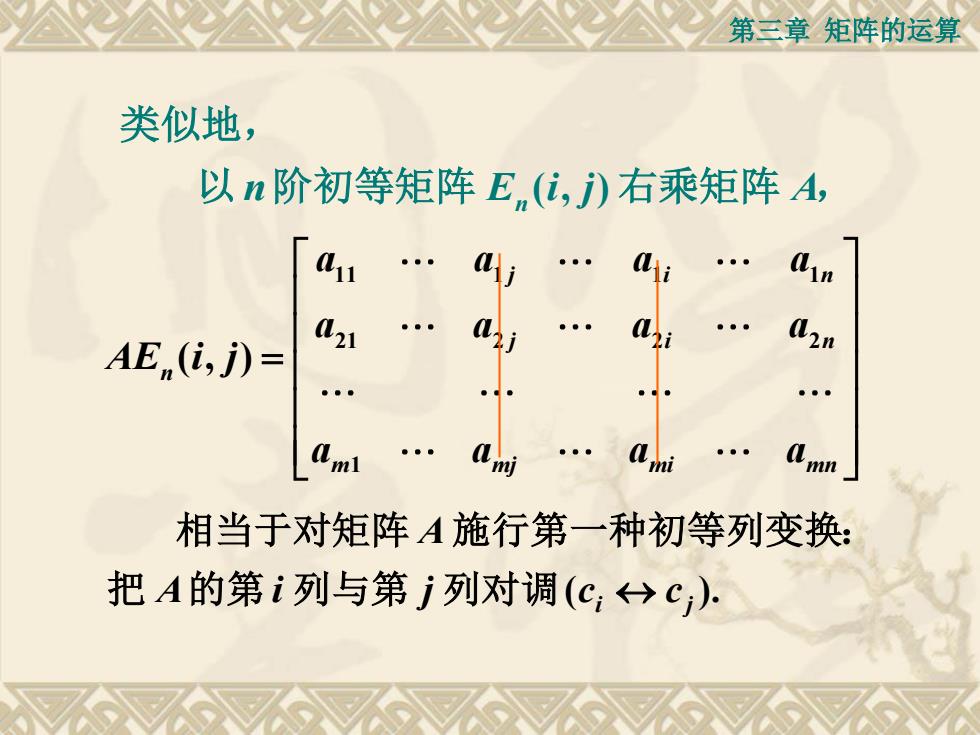
第三章矩阵的运算 类似地, 以n阶初等矩阵E,(亿,)右乘矩阵A, AE (i,j)= l21 。 mi 相当于对矩阵A施行第一种初等列变换: 把A的第i列与第j列对调(c,)C):
第三章 矩阵的运算 ( , ) n E i j A n 类似地, 以 阶初等矩阵 右乘矩阵 , 11 1 1 1 21 2 2 2 1 ( , ) j i n j i n n m mj mi mn a a a a a a a a AE i j a a a a = ( ). i j A i j c c A 把 的第 列与第 列对调 相当于对矩阵 施行第一种初等列变换: