
例4.已知函数y=了x)={2yx, 0≤x≤1 11+x, x>1 求f()及f(),并写出定义域及值域 解:f(2)=23=√2 0<t<1 t≤0时 2 函数无定义 t≥1 定义域D=[0,+o) 值域f(D)=[0,+o〉 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例4. 已知函数 + = = 1 , 1 2 , 0 1 ( ) x x x x y f x 求 ( ) 2 1 f 及 ( ), 1 t f 解: 2 1 2 1 f ( ) = 2 = 2 ( ) = 1 t f , 0 t 1 1 1 t + , t 1 2 t t 0 时 函数无定义 并写出定义域及值域 . 定义域 D = [0, + ) 值 域 f (D) = [0, + ) 机动 目录 上页 下页 返回 结束

2.函数的几种特性 设函数y=f(x),x∈D,且有区间IcD (1)有界性 Vx∈D,3M>0,使f(x)≤M,称f(x)为有界函数 Vx∈I,3M>0,使f(x)≤M,称f(x)在I上有界 说明:还可定义有上界、有下界、无界(见上册P6) (2)单调性 Vx1,x2∈1,x1<x2时, 若f(x)<f(x2),称f(x)为I上的 单调增函数; 若f(x)>f(x2),称f(x)为I上的 X2 单调减函数 HIGH EDUCATION PRESS 机动目录上页下页返回结束
2. 函数的几种特性 设函数 y = f (x) , x D , 且有区间 I D . (1) 有界性 x D , M 0, 使 f (x) M , 称 f (x) x I , M 0, 使 f (x) M , 称 f (x) 说明: 还可定义有上界、有下界、无界 (见上册 P6 ) (2) 单调性 为有界函数. 在 I 上有界. 若对任意正数 M , 均存在 x D, 使 f (x) M , 则称 f ( x ) 无界. 称 为有上界 称 为有下界 , f ( x) M , , M f ( x), x1 , x2 I, 当 1 2 x x 时, ( ) ( ), 1 2 若 f x f x 称 f (x) 为 I 上的 ( ) ( ), 1 2 若 f x f x 称 f (x) 为 I 上的 单调增函数 ; 单调减函数 . x y 1 x 2 x 机动 目录 上页 下页 返回 结束

(3)奇偶性 Vx∈D,且有-x∈D 若f(-x)=f(x),则称fx)为偶函数: 若f(-x)=-f(x),则称fx)为奇函数 说明:若f(x)在x=0有定义,则当 f(x)为奇函数时,必有f(0)=0. 例如, y=8x-x2-10 y=5tanx HIGH EDUCATION PRESS e0C8 机动目录上页下页返回结束
x y − x o x (3) 奇偶性 x D, 且有 − x D, 若 则称 f (x) 为偶函数; 若 则称 f (x) 为奇函数. 说明: 若 f (x) 在 x = 0 有定义 , f ( x) 为奇函数时, f (0) = 0. 则当 必有 例如, 机动 目录 上页 下页 返回 结束 4 2 y 8x x 10 y 5tan x = − − =
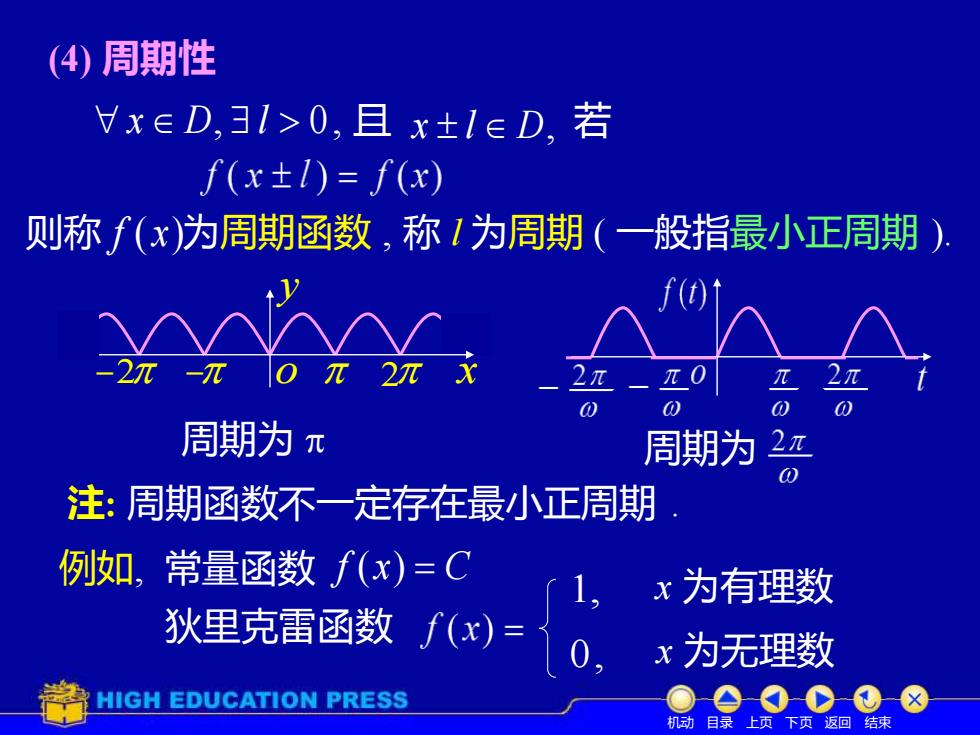
(4)周期性 Vx∈D,3l>0,且x±l∈D,若 f(x±I)=f(x) 则称f(x)为周期函数,称1为周期(一般指最小正周期) "(t -2-0 0 0 周期为元 周期为2π 注:周期函数不一定存在最小正周期 例如,常量函数f(x)=C 1 。x为有理数 狄里克雷函数f(x)= 0,x为无理数 HIGH EDUCATION PRESS 机动目录上页下页返回结束
(4) 周期性 x D, l 0, 且 x l D, 则称 f ( x) 为周期函数 , 2 − o x y − 2 若 称 l 为周期 ( 一般指最小正周期 ). 周期为 周期为 注: 周期函数不一定存在最小正周期 . 例如, 常量函数 f (x) = C 狄里克雷函数 x 为有理数 x 为无理数 1, 0, 机动 目录 上页 下页 返回 结束