
第之为 第一章 极限存在准则及 两个重要极限 极限存在准则 夹逼准则单调有界准则 二、两个重要极限 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、 两个重要极限 一、极限存在准则 夹逼准则 单调有界准则 第六节 机动 目录 上页 下页 返回 结束 极限存在准则及 两个重要极限 第一章

1、数列的夹逼准则C准则1)P46 (0)yn≤xm≤2n(n=1,2,.) =>lim xn a (2)lim yn lim zn a n→o0 n→oo 证:由条件(2),V8>0,3N1,N2, 当n>N1时,yn-a<8 当n>N2时,2m-a<8 令N=max{N1,N2},则当n>N时,有 a-8<ym<a+8,a-8<2n<a+8, 由条件(1) a-E≤yn≤Xn≤2n<a+8 即xn-a<6,故lim=a. n-→∞ HIGH EDUCATION PRESS 机动目录上页下页返回结束
y z a n n n n = = → → (2) lim lim 1、数列的夹逼准则(准则1)(P46) (1) y x z ( n = 1, 2, ) n n n x a n n = → lim 证:由条件 (2) , 0, , N1 当 时, 当 时, 令 max , , N = N1 N2 则当 n N 时, 有 由条件 (1) n n n a − y x z a + 即 x − a , n 故 lim x a . n n = → , N2 机动 目录 上页 下页 返回 结束
准则1.当x∈U(x,δ)时,8(x)≤f(x)≤h(x),且 (x>X>0) lim g(x)=lim h(x)=4 x→x0 X→x0 (x-→0)】 (x→∞) lim f(x)=A x→x0 (x→>o0 HIGH EDUCATION PRESS eOC①8 机动目录上页下页返回结束
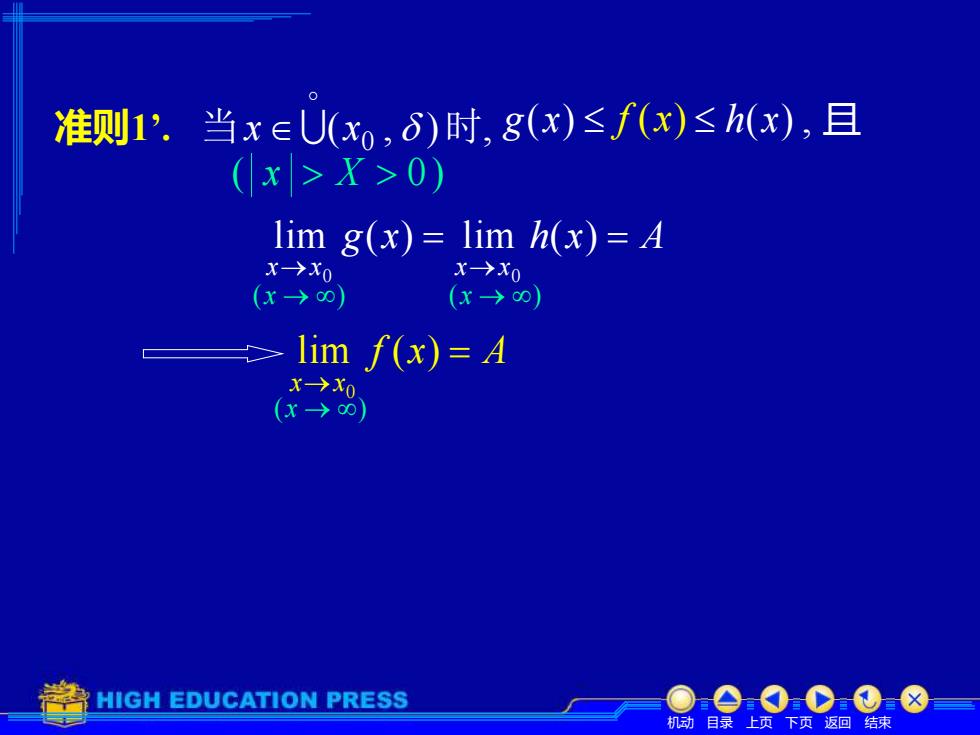
机动 目录 上页 下页 返回 结束 准则1’. g x h x A x x x x = = → → lim ( ) lim ( ) 0 0 g(x) f (x) h(x) , f x A x x = → lim ( ) 0 ( x X 0 ) (x → ) (x → ) (x → ) 当x (x0 , )时, 且

重要极限 1.lim sinx =1 x→0 证:当x∈(0,)时, △AOB的面积<圆扇形AOB的面积<AAOD的面积 即 sinx <tanx 故有 1< 1 sin x (0<x<) sin x 显然有 COSx< ∠1 (0<x<) X lim cosx=1,注 sin x lim x->0 x>0 HIGH EDUCATION PRESS 注目录上页下页返回结束
1 sin cos x x x 圆扇形AOB的面积 重要极限 证: 当 即 sin x 2 1 tan x 2 1 亦即 sin tan (0 ) 2 x x x x (0, ) 2 x 时, (0 ) 2 显然有 x △AOB 的面积< <△AOD的面积 D C B A x 1 o 故有 注 注 目录 上页 下页 返回 结束

例2.求1im tan x x→0X 解: lim tan x sinx lim x→0 x-→0 X COS X sinx lim x-→0x f = x-→0C0Sx 例3.求1im arcsin x x→0 X 解:令t=arcsinx,则x=sint,因此 原式=lim,=lim =1 t-→0Slnt t→0 sint HIGH EDUCATION PRESS eOC①8 机动目录上页下页返回结束
例2. 求 解: x x x tan lim →0 = → x x x x cos sin 1 lim 0 x x x sin lim →0 = x cos x 1 lim →0 =1 例3. 求 解: 令 t = arcsin x , 则 x = sin t , 因此 原式 t t t sin lim →0 = t sin t =1 机动 目录 上页 下页 返回 结束