《线性代数》课程教学课件（PPT讲稿，B）第五章 相似矩阵与二次型 §5.1 向量的内积与正交向量组

第五章相似矩阵与二次型 Ch5 相似矩阵与二次型 ·§5.1向量的内积与正交向量组 ·§5.2方阵的特征值与特征向量 §5.3相似矩阵 ·§5.4实对称矩阵的相似对角形 ·§5.5二次型及其标准型 。§5.6正定二次型

第五章 相似矩阵与二次型 Ch5 相似矩阵与二次型 §5.2 方阵的特征值与特征向量 §5.1 向量的内积与正交向量组 §5.3 相似矩阵 §5.4 实对称矩阵的相似对角形 §5.5 二次型及其标准型 §5.6 正定二次型

第五章相似矩阵与二次型 §5.1向量的内积及正交向量组 内积的定义及性质 二、 向量的长度及性质 三、 正交向量组的概念及求法 四、正交矩阵与正交变换 五、小结思考题

第五章 相似矩阵与二次型 二、向量的长度及性质 五、小结 思考题 三、正交向量组的概念及求法 四、正交矩阵与正交变换 一、内积的定义及性质 §5.1 向量的内积及正交向量组

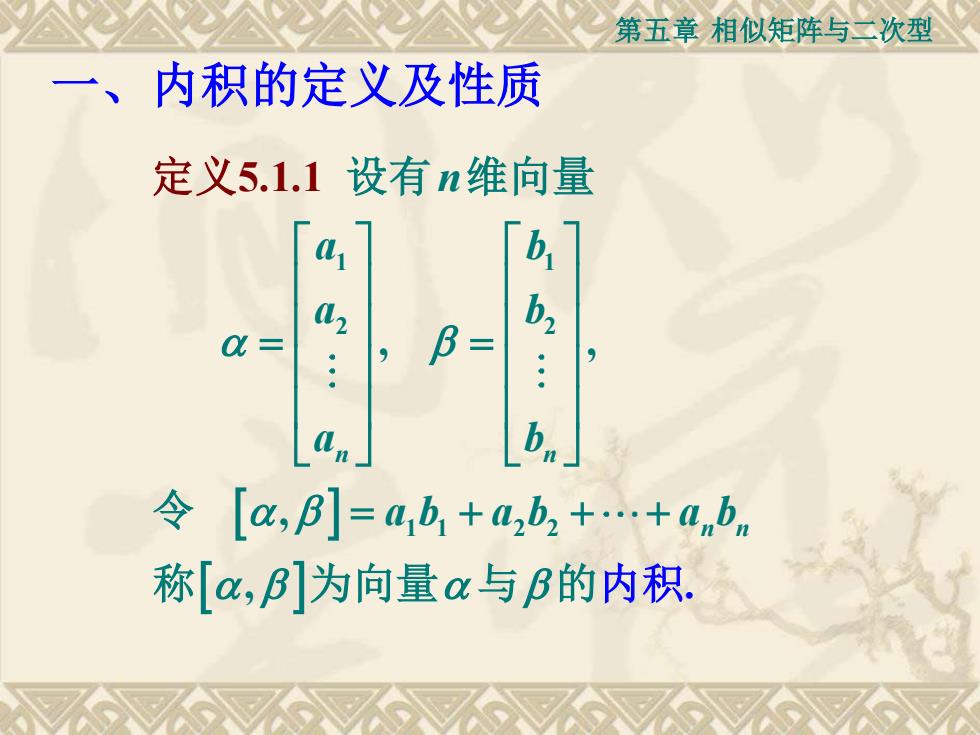
第五章相似矩阵与二次型 一、内积的定义及性质 定义5.1.1 设有n维向量 42 B= b2 0= 令[a,B]=b1+,b2+.+anbn 称[a,B]为向量au与β的内积

第五章 相似矩阵与二次型     1 1 2 2 1 1 2 2 5.1 , , , . , 1 . n n n n n a b a b a b a b a b a b                     = =             = + + + 设有 维向量 令 称 为向量 与 定 的内积 义 一、内积的定义及性质

第五章相似矩阵与二次型 说明： 1. n≥4)维向量的内积是3维向量数量积 的推广，但是没有3维向量直观的几何意义. 2.内积是向量的一种运算，如果a,B都是列 向量，内积可用矩阵记号表示为： [a,β]=ap

第五章 相似矩阵与二次型 说明: 1. n(n≥4)维向量的内积是3维向量数量积 的推广，但是没有3维向量直观的几何意义．   2. , , , : , .       =  内积是向量的一种运算 如果 都是列 向量 内积可用矩阵记号表示为

第五章相似矩阵与二次型 内积的运算性质 (其中a,B,y为n维向量，为实数)： [aB]=[B,a]; (2)[a,B]=[a,B]: (3)[a+B,r]=[a,r]+[B,y]: (4)[a,a]≥0，且当a≠0时有a,a]>0. schwarz不等式[a,B≤[a,alB,B]

第五章 相似矩阵与二次型 内积的运算性质 (其中    , , , : 为n维向量 为实数) (1) , , ;      =   (2) , , ;       =   (3) , , , ;        + = +      (4) [ , ] 0, 0 [ , ] 0.         且当 时有 2 schwarz不等式 [ , ] [ , ][        , ]