
第一章 盖数与极民 函数一 研究对像 分析基础 极限一 研究方法 连续一 研究桥梁
第一章 分析基础 函数 极限 连续 — 研究对象 — 研究方法 — 研究桥梁 函数与极限

第一章 第一节 联射与盖教 一、 映射 二、函数 HIGH EDUCATION PRESS 机动目录上页下页返回结束
第一章 二、函数 一、映射 第一节 机动 目录 上页 下页 返回 结束 映射与函数

映射 1.映射的概念 定义.设X,Y是两个非空集合,若存在一个对应规 则f,使得Hx∈X,有唯一确定的y∈Y与之对应,则 称f为从X到Y的映射,记作f:X→Y 元素y称为元素x在映射f下的像,记作y=f(x) 元素x称为元素y在映射f下的原像 集合X称为映射f的定义域,D, Y的子集f(X)={f(x)x∈X}称为f的值域.R HIGH EDUCATION PRESS e0C⊙8 机动目录上页下页返回结束
定义. 设 X , Y 是两个非空集合, 若存在一个对应规 则 f , 使得 有唯一确定的 与之对应 , 则 称 f 为从 X 到 Y 的映射, 记作 f : X → Y . 元素 y 称为元素 x 在映射 f 下的 像 , 记作 y = f ( x). 元素 x 称为元素 y 在映射 f 下的 原像 . 集合 X 称为映射 f 的定义域 ; Y 的子集 f (X ) = f (x) x X 称为 f 的 值域 . X f Y 机动 目录 上页 下页 返回 结束 Rf Df 一、 映射 1. 映射的概念
注意:1)映射的三要素一定义域,对应规则,值域 2)元素x的像y是唯一的,但y的原像不一定唯一 对映射f:X→Y 若f(X)=Y,则称f为满射 Y=f(x) 若V6,x2∈X,x1≠x2,有 f(x)≠∫(x2】 则称f为单射; f(X 若f既是满射又是单射,则称f为双射或一一映射 HIGH EDUCATION PRESS 机动目录上页下页返回结束
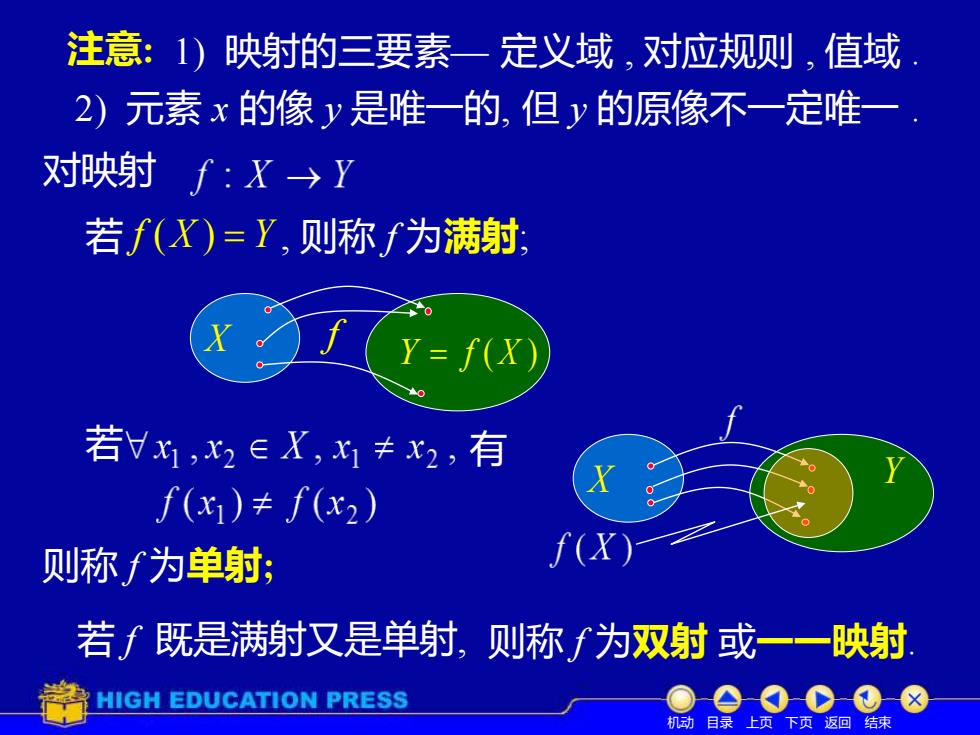
对映射 若 f (X ) = Y , 则称 f 为满射; X Y f = f ( X ) 若 有 则称 f 为单射; 若 f 既是满射又是单射, 则称 f 为双射 或一一映射. X Y 机动 目录 上页 下页 返回 结束 注意: 1) 映射的三要素— 定义域 , 对应规则 , 值域 . 2) 元素 x 的像 y 是唯一的, 但 y 的原像不一定唯一

说明: 映射又称为算子在不同数学分支中有不同的惯用 名称例如, X(卡☑ Y(数集) f称为X上的泛函 X(卡☑ f称为X上的变换 X(数集或点集) 一R 称为定义在X上的为函数 HIGH EDUCATION PRESS 机动目录上页下页返回结束
X (数集 或点集 ) 说明: 在不同数学分支中有不同的惯用 X (≠ ) Y (数集) 机动 目录 上页 下页 返回 结束 f f 称为X 上的泛函 X (≠ ) X f f 称为X 上的变换 R f f 称为定义在 X 上的为函数 映射又称为算子. 名称. 例如