
第一章 第二节 教列的教很 一、 数列极限的定义 二、收敛数列的性质 HIGH EDUCATION PRESS 机动目录上页下页返回结束
第一章 二 、收敛数列的性质 一、数列极限的定义 第二节 机动 目录 上页 下页 返回 结束 数列的极限

一、数列极限的定义 引例.设有半径为r的圆,用其内接正边形的面积 A,逼近圆面积S. 如图所示,A,为内接正三边形面积, A,为内接正六边形面积,等等 当n无限增大时,An无限逼近S刘徽割圆术), 数学语言描述:V&>0,3正整数N,当n>N时,总有 |4n-SKε HIGH EDUCATION PRESS 0◆0C08 刘徽目录上页下页返回结束
数学语言描述: 一 、数列极限的定义 引例. 设有半径为 r 的圆 , 逼近圆面积 S . 如图所示 , 当 n 无限增大时, 无限逼近 S (刘徽割圆术) , 0 , 正整数 N , 当 n > N 时, A − S n 用其内接正 n 边形的面积 总有 刘徽 目录 上页 下页 返回 结束 为内接正三边形面积, 为内接正六边形面积,等等

定义:自变量取正整数的函数称为数列,记作xn=f(n) 或{xn}.xn称为通项(一般项) 2,4,82.,2”,. 2”} 111 2’4’8, 1,-1,1,.,(-1)m1,. (-1)”-1} 4E0:+少 ’3 √3,V3+√3,.,V3+V3+V.+V3,. HIGH EDUCATION PRESS
定义: 自变量取正整数的函数称为数列, 记作 或 称为通项(一般项) . 2,4,8, ,2 , ; n , ; 2 1 , , 8 1 , 4 1 , 2 1 n {2 } n } 2 1 { n 1, 1,1, ,( 1) , ; − − n+1 {( 1) } −1 − n , ; ( 1) , , 3 4 , 2 1 2, 1 n n n− + − } ( 1) { 1 n n n− + − 3, 3 + 3, , 3 + 3 + + 3 ,
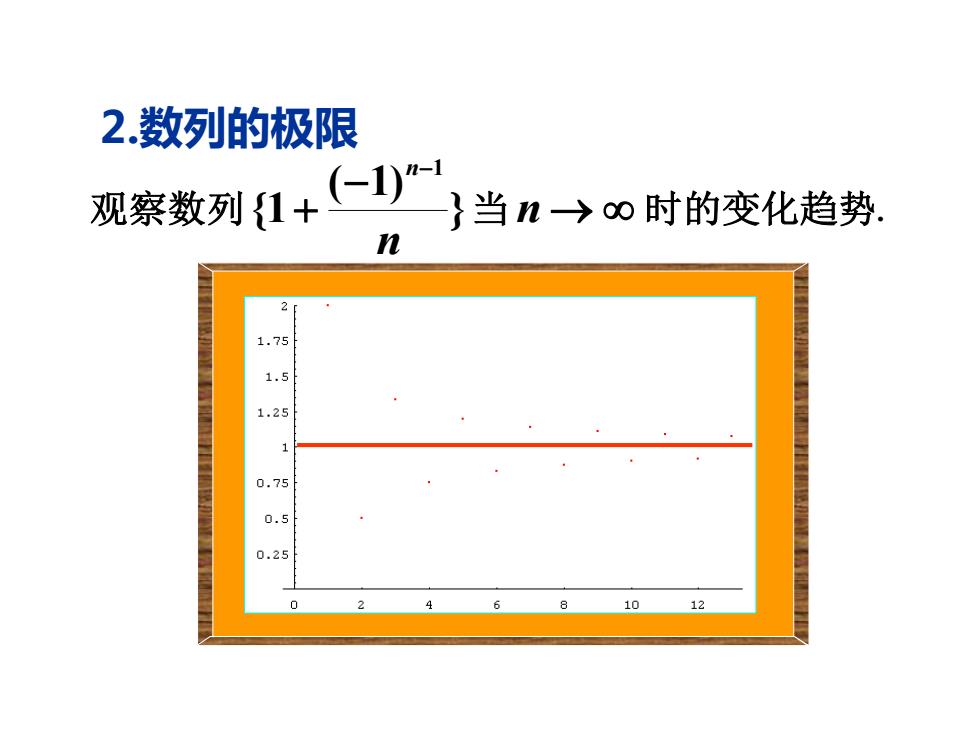
2数列的极限 观察数列1+一) 一}当n→oo时的变化趋势. n 1.75 1.5 1.25 0.75 0.5 0.25 10 12
观察数列 当 → 时的变化趋势. − + − n n n } ( 1) {1 1 2.数列的极限

定义:如果当无限增大时,数列{x,的通项xm 无限趋近于某一确定常数a,则称a为数 列{x,},当n趋于无穷大时的极限,记作 imxn三4,或xm→4(n→o) 1->oo 此时也称该数列收敛; 若不存在,则称数列发散。 HIGH EDUCATION PRESS
定义:如果当 n 无限增大时,数列 xn 的通项 n x 无限趋近于某一确定常数 a ,则称 a 为数 lim = , → ( → ) → xn a n a n n 或 x 此时也称该数列收敛; 若 a 不存在,则称数列发散。 列 xn ,当 n 趋于无穷大时的极限,记作