
2.逆映射与复合映射 (1)逆映射的定义 定义:若映射f:Df(D)为单射,则存在一新映射 f1:f(D)→D,使yef(D),f(y)=x,其中f(x)=y, 称此映射f为f的逆映射 习惯上,y=f(x),x∈D 的逆映射记成 y=f'(x),x∈f(D) 例如,映射y=x2,x∈(-0,0],其逆映射为 y=-√/x,x∈[0,+0) HIGH EDUCATION PRESS 机动目录上页下页返回结束
2. 逆映射与复合映射 (1) 逆映射的定义 定义: 若映射 为单射, 则存在一新映射 使 习惯上 , y = f (x), x D 的逆映射记成 ( ) , ( ) 1 y = f x x f D − 例如, 映射 其逆映射为 D f (D) f −1 f 其中 称此映射 −1 f 为 f 的逆映射 . 机动 目录 上页 下页 返回 结束
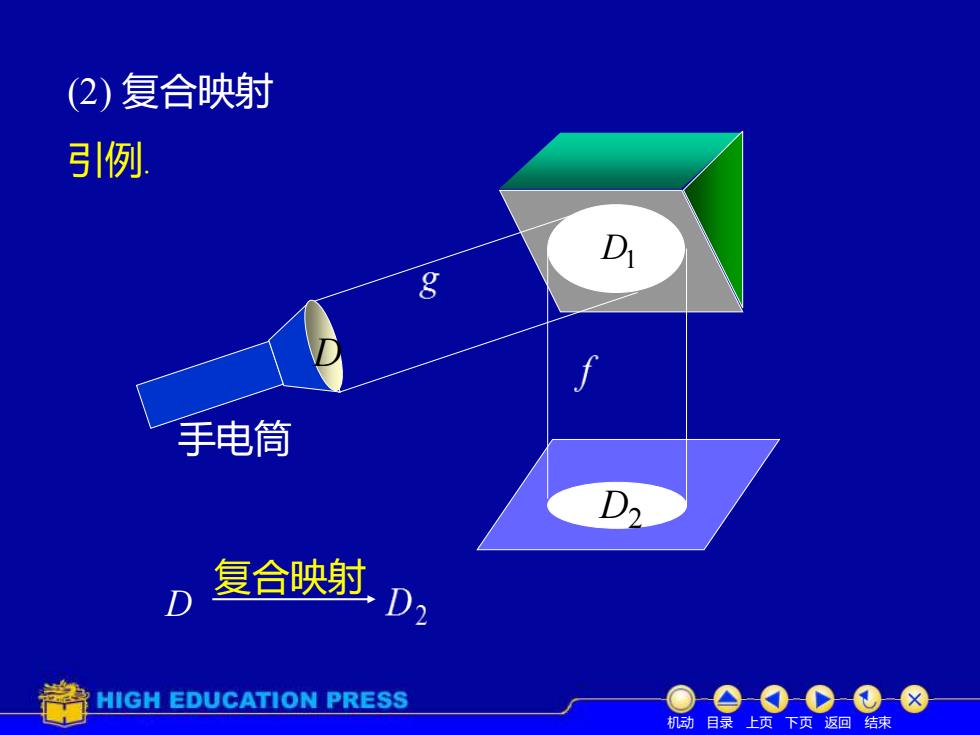
(2)复合映射 引例. D 手电筒 复合映射 D HIGH EDUCATION PRESS e0C①8 机动目录上页下页返回结束
(2) 复合映射 机动 目录 上页 下页 返回 结束 D1 手电筒 D D D2 引例. 复合映射
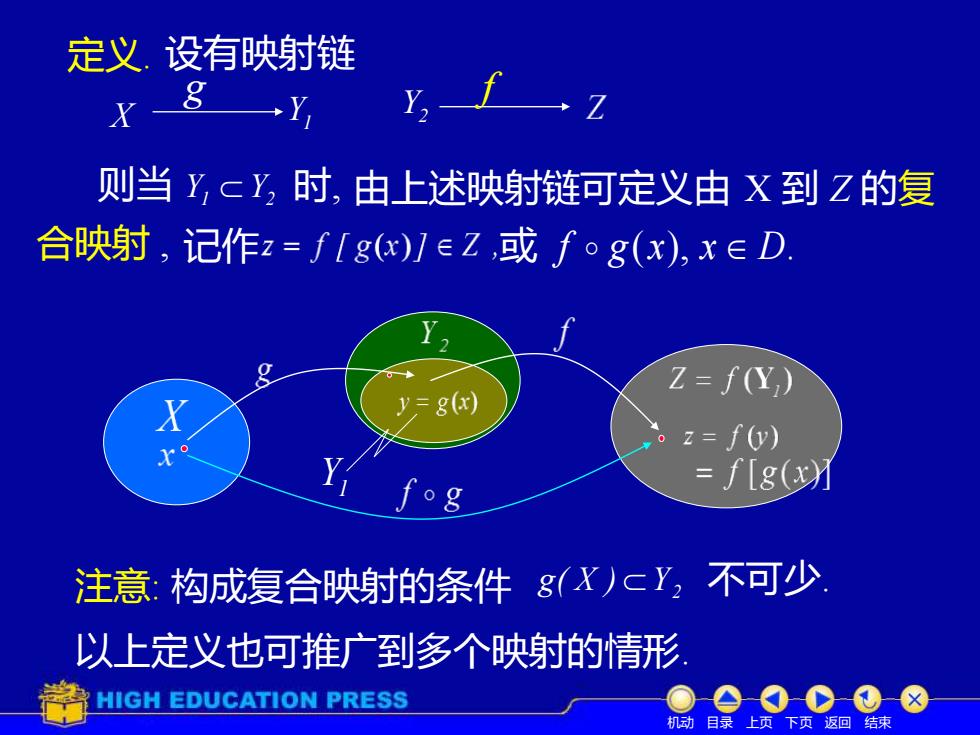
定义设有映射链 X 8 →Y) 则当ycY,时,由上述映射链可定义由X到Z的复 合映射,记作z=fIg)]∈Z或fog(x),x∈D Z=f(Y) g(x z=f(y) Y =f[g( 注意:构成复合映射的条件gX)cY,不可少 以上定义也可推广到多个映射的情形 為HIGH EDUCATION PRESS 机动目录上页下页返回结束
定义. X g Y1 Y2 f 则当 Y Y 1 2 由上述映射链可定义由 X 到 Z 的复 f g(x), x D. 设有映射链 合映射 , 记作 时, 或 Y1 机动 目录 上页 下页 返回 结束 注意: 构成复合映射的条件 2 g( X ) Y 不可少. 以上定义也可推广到多个映射的情形

二、函数 1.函数的概念 定义4.设数集DcR,则称映射f:D→R为定义在 D上的函数,记为 定义域 y=f(x),x∈D 因变量 自变量 f(D)称为值域R, 函数图形: C={(x,y)y=f(x),x∈D》 a X (D=[a,b]) HIGH EDUCATION PRESS 0eOC①8 机动目录上页下页返回结束
定义域 二、函数 1. 函数的概念 定义4. 设数集 D R , 则称映射 为定义在 D 上的函数 , 记为 y = f (x), x D f ( D ) 称为值域 函数图形: C = (x , y) y = f (x ) , x D x y ( D = [ a , b ] ) a x b y 机动 目录 上页 下页 返回 结束 因变量 自变量 Rf

一y∈f(D)={yy=f(x),x∈D》 (定义域) (对应规则 (值域 定义域 使表达式及实际问题都有意义的自变量 集合 •对应规律的表示方法: 解析法、图像法、列表法 例如,反正弦主值y=∫(x)=arcsin x 定义域D=【-1,1],值域/(D)=[-受,受] x,x≥0 又如绝对值函数1过==Xx<0 定义域D=R 值域f(D)=[0,+o) 0 HIGH EDUCATION PRESS 机动目录上页下页返回结束
x D f y f (D) = y y = f ( x), x D (定义域) (对应规则) (值域) 例如, 反正弦主值 • 定义域 • 对应规律的表示方法: 解析法 、图象法、列表法 使表达式及实际问题都有意义的自变量 集合. 定义域 值域 又如, 绝对值函数 定义域 值 域 机动 目录 上页 下页 返回 结束