《数字信号处理》课程教学课件（PPT讲稿）ch2_2 DFT性质

离散傅里叶变换的性质1.线性DFT (ax,[k] + bx2[k]}= aDFT (x[k]})+ bDFT (x2[k])需将较短序列补零后，再按长序列的点数做DFT2.循环位移（Circularshiftof a sequence）循环位移定义为y[k] = x[(k +n)~]R[k]

离散傅里叶变换的性质 1. 线性 DFTax1 [k]+ bx2 [k]= aDFTx1 [k]+ bDFTx2 [k] 需将较短序列补零后，再按长序列的点数做DFT 2. 循环位移(Circular shift of a sequence) y[k] x[(k n) ]R [k] = + N N 循环位移定义为

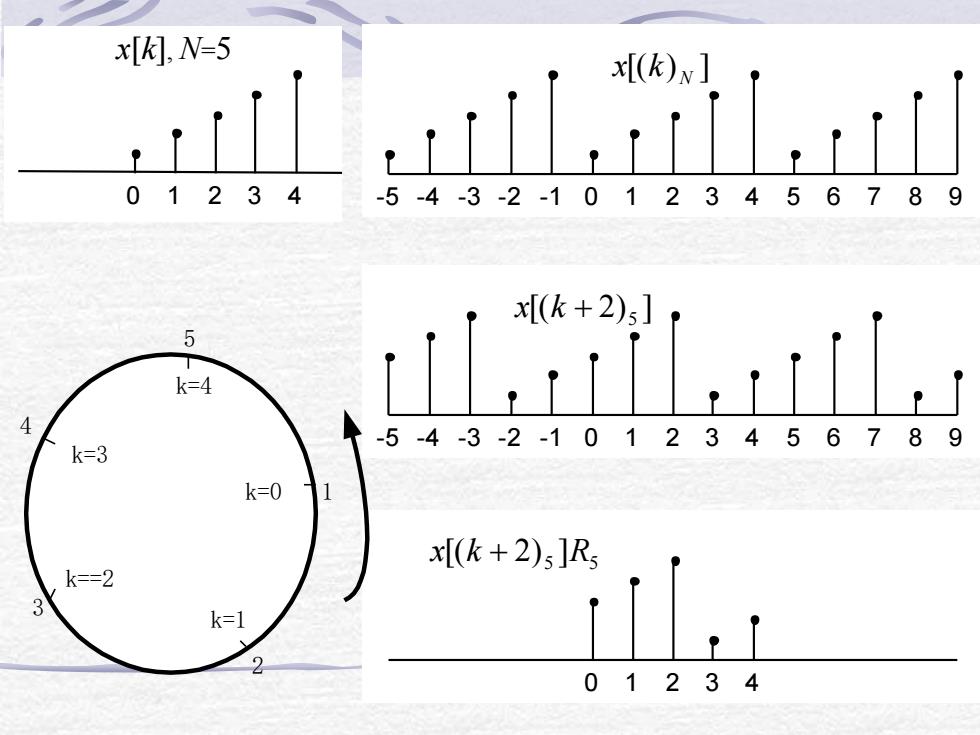
x[K], N=5x[(k)n ]32402856720295.3-1475k=445678O230k=3k=0x[(k + 2)s]Rk==2k=102732

x[k], N=5 0 1 2 3 4 [( ) ] N x k -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 [( 2) ] + 5 x k -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 5 5 x[(k + 2) ]R 0 1 2 3 4 1 5 4 3 2 k=0 k==2 k=1 k=4 k=3

DFT时域循环位移特性·DFS(x[k + n]} = W-mn X[m]DFT(x[(k +n)]R[K])= Wmn X[m]DFT频域循环位移特性. DFS(Wkx[k] = X[m + ]]DFT(wkx[K]= X[(m+ 1) JR[m]

[ ] ~ [ ]} ~ DFS{x k n W X m mn N − • + = DFTx[(k n) ]R [k] W X[m] mn N N N − + = [ ] ~ [ ]} ~ DFS{W x k X m l lk • N = + DFTW x[k] X[(m l) ]R [m] N N l k N = + DFT时域循环位移特性 DFT频域循环位移特性

3.对称性（symmetry）周期共轭对称(Periodic conjugate symmetry)定义为x[k] = x*[(-k)~]R~[k] = x*[N -k]周期共轭反对称(Periodic conjugate antisymmetry)定义为x[k] = -x*[(-k)~]R[k] = -x *[N - k]当序列x[K为实序列时，周期偶对称序列满足x[k] = x[N -k]当序列x[K为实序列时，周期奇对称序列满足x[k] =-x[N -k]

3. 对称性(symmetry) 周期共轭对称(Periodic conjugate symmetry)定义为 周期共轭反对称(Periodic conjugate antisymmetry)定义为 x[k] x*[( k) ]R [k] x*[N k] = − N N = − x[k] x*[( k) ]R [k] x*[N k] = − − N N = − − 当序列x[k]为实序列时，周期偶对称序列满足 x[k] = x[N − k] 当序列x[k]为实序列时，周期奇对称序列满足 x[k] = −x[N − k]

对称特性·DFS(x*[k]} = X*[-m]1DFT(x*[k]} = X*[(-m)]R[m]·DFS[x*[-k]} = X*[m]1DFT(x*[(-k)]R~[k]} = X*[m]当x[k]是实序列时X[m] = X*[(-m) ]R[k]

对称特性 [ ] ~ [ ]} ~ • DFS{x k = X −m   [ ] ~ [ ]} ~ DFS{x k X m   • − = [ ] ~ DFT{x [( k) N ]RN [k]} X m   − = DFT{x [k]} X [( m) ]R [m] = − N N   当x[k]是实序列时 X[m] X [( m) ]R [k] = − N N 