apnpubBseuquency(Hz理论分析如下:按x(t)=1-cos(t)+2sin(2πt)+cos(3元πt)o+e-j2wgtj3wot +e-j3wofeo+e-mo=1222j故得:1,n=0-1/2,n= ±1X(k@o)=-+j, n= ± 21/2,n=± 30,其他可见,MATLAB作出的幅频特性与理论分析很吻合。例3:Xr(t)为幅度A=10,周期To=1秒,脉冲宽度t=0.2秒的周期脉冲串。1)计算基波和多少次谐波的功率和可以占信号总功率的90%以上。2)作N=256点的fft,计算其频谱。查看直流及各次谐波k=0.1,2...的幅度。为3)便于观察,在[一30Hz,30Hz]内绘出其频谱。解:1)周期信号是功率信号,信号总功率为: r"g1 X,(0)P dt = f02 102 dt = 200=理论分析该信号的频谱为:
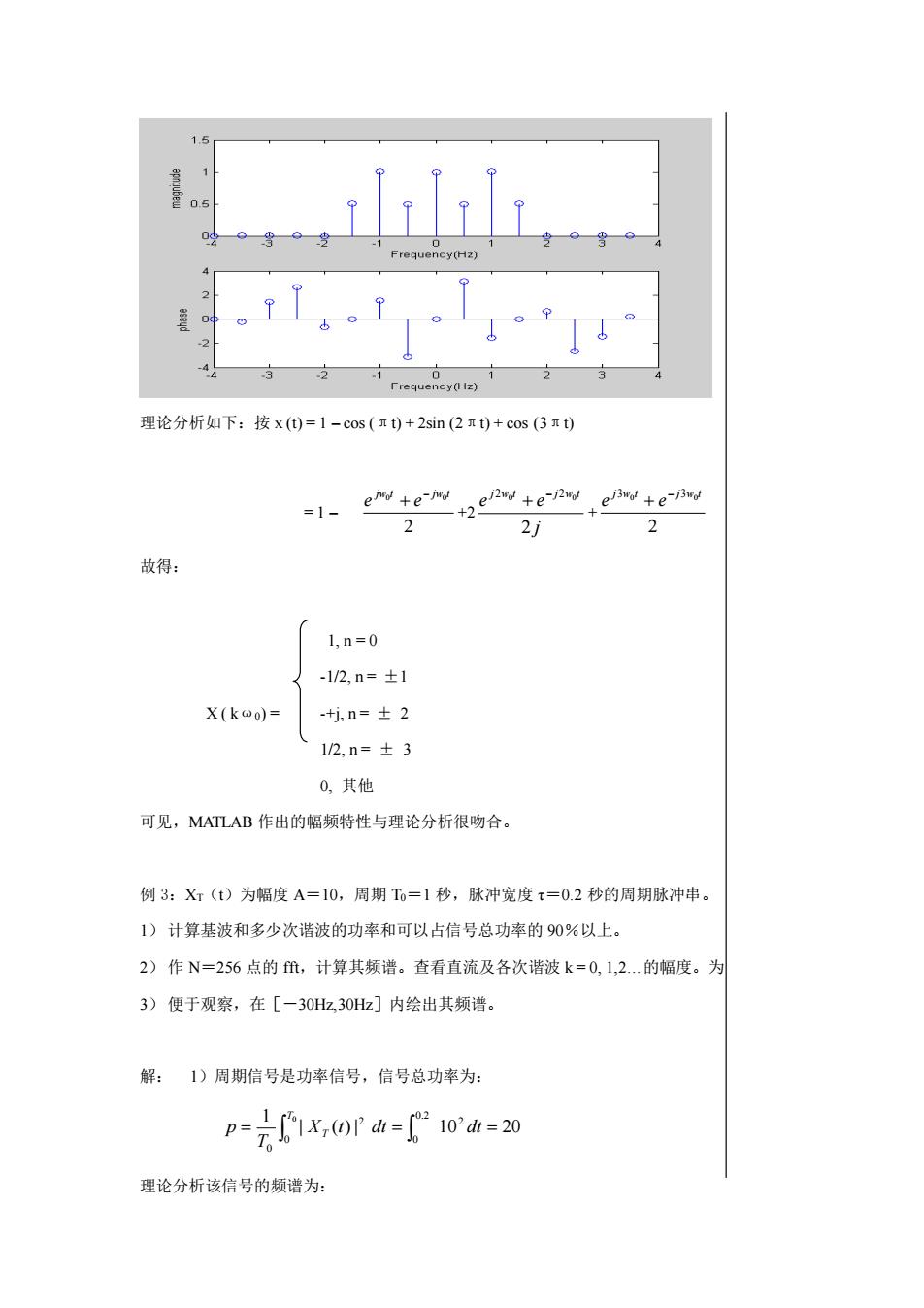
理论分析如下:按 x (t) = 1 – cos (πt) + 2sin (2πt) + cos (3πt) = 1 – 2 0 0 jw t jw t e e − + +2 j e e j w t j w t 2 2 0 − 2 0 + + 2 3 0 3 0 j w t j w t e e − + 故得: 1, n = 0 -1/2, n = ±1 X ( kω0) = -+j, n = ± 2 1/2, n = ± 3 0, 其他 可见,MATLAB 作出的幅频特性与理论分析很吻合。 例 3:XT(t)为幅度 A=10,周期 T0=1 秒,脉冲宽度 τ=0.2 秒的周期脉冲串。 1) 计算基波和多少次谐波的功率和可以占信号总功率的 90%以上。 2) 作 N=256 点的 fft,计算其频谱。查看直流及各次谐波 k = 0, 1,2.的幅度。为 3) 便于观察,在[-30Hz,30Hz]内绘出其频谱。 解: 1)周期信号是功率信号,信号总功率为: | ( ) | 10 20 1 2 0.2 0 2 0 0 0 = = = X t dt dt T p T T 理论分析该信号的频谱为:

X(kwo)=(At / To)Sa((k@ot)/2=2Sa(0.2k)下面计算前2k+1项的总功率:k=input(k=);n=-k:k,x=2*sinc(0.2*n);pO=20;p=sum(x.±2)/po基波和前5次谐波的功率之和占信号90%以上的能量。XT(t)的傅里叶级数:Xr (t) =2 + 1.87ej0 +1.51ei2ot+1.01ej30t++1.87e-j"0t +1.51e-j201+1.01e-j3ot...2)计算N=256点的FFT,基波和前127次谐波所包含的能量占总能量的99.6%。N=256;T0=1; T=T0/N;(=0:T:TO; %t=-TO/2:T:TO /2;x=5*[square(2*pi*(t+0.1),20)+1];X=1/N*fft(x,N);f=1/T/N*(-30:30);%在[-30Hz,30Hz]内绘出其频谱。subplot(2,1,1); plot(t,x); xlabel(Time (s)"); ylabel(Amplitude')title('square wave and its spectrum');y=abs(fftshift(X);subplot(2,1,2); stem (f,y(129-30:129+30),xlabel(Frequency(Hz)); ylabel('Magnitude');
X(kω0) = (Aτ / T0)Sa((kω0τ)/2 = 2Sa(0.2kπ) 下面计算前 2k + 1 项的总功率: k=input('k='); n=-k:k; x=2*sinc(0.2*n); p0=20; p=sum(x.^2)/p0 基波和前 5 次谐波的功率之和占信号 90%以上的能量。 XT(t)的傅里叶级数: XT(t)=2 + 1.87 ejω0t + 1.51ej2ω0t + 1.01ej3ω0t + . + 1.87 e - jω0t + 1.51 e - j2ω0t + 1.01e - j3ω0t . 2)计算 N=256 点的 FFT, 基波和前 127 次谐波所包含的能量占总能量的 99.6%。 N=256;T0=1; T=T0/N; t=0:T:T0; %t = -T0 / 2: T: T0 / 2; x=5*[square(2*pi*(t+0.1),20)+1]; X=1/N*fft(x,N); f=1/T/N*(-30:30) ; %在[ -30Hz, 30Hz]内绘出其频谱。 subplot(2,1,1); plot(t,x); xlabel('Time (s)'); ylabel('Amplitude'); title('square wave and its spectrum'); y=abs(fftshift (X)); subplot(2,1,2); stem (f,y(129-30:129+30)); xlabel('Frequency(Hz)'); ylabel('Magnitude');