
3.u=f()=e=x2siy,uou Ox'ay 解 u_y+[. Ox Ox'8z Ox =2e+y2+:+2e2+y+22 xsin y =2x(1+2x2sin2 y)extxsin2y ou_ofof Bz 8yay oz by =2ye+2++2e2+.x2 ·x-cos y =2(y+xsin ycosy)etsi HIGH EDUCATION PRESS 机动目录上页下页返回结束
例3. ( , , ) , sin , 2 2 2 2 u f x y z e z x y x y z = = = + + y u x u 求 , 解: x u 2 2 2 2 x y z xe + + = x y x y x x y e 2 2 4 2 2 2 sin 2 (1 2 sin ) + + = + x y z x y u y u 2 2 2 2 x y z ye + + = x y x y y x y y e 2 2 4 2 4 sin 2 ( sin cos ) + + = + x f = 2 2 2 2 x y z ze + + + y f = y z z f + 2 2 2 2 x y z ze + + + 2 x sin y x cos y 2 机动 目录 上页 下页 返回 结束
主观题10分 g设置 2西 2.设z=fx,y,w)=e"sinx+y),u=y求0 正常使用主观题需2.0以上版本雨课堂 HIGH EDUCATION PRESS 作答
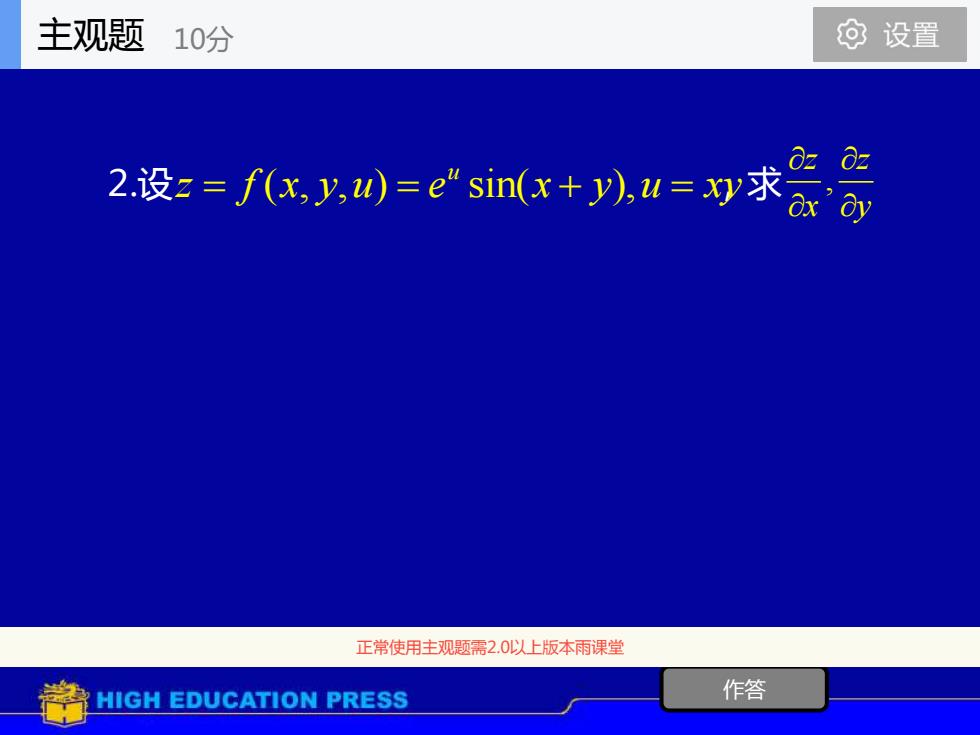
2.设 ,求 作答 正常使用主观题需2.0以上版本雨课堂 ( , , ) sin( ), u z f x y u e x y u xy = = + = , z z x y 主观题 10分

例4.设z=w+sint,u=e',v=cost,求全导数 d 解: dz Oz du,Oz dv Oz dt"ou dt Ov dt Ot =ve-usint cost =e'(cost-sint)+cost HIGH EDUCATION PRESS D◆0C08 机动目录上页下页返回结束
例4. 设 z = uv + sin t , . d d t z z u v t t t t z d d t = v e e t t t t = (cos − sin ) + cos t u u z d d = t z + u = e t , v = cost , 求全导数 解: + cost 机动 目录 上页 下页 返回 结束

例5.设w=f(x+y+2,xyz),f具有二阶连续偏导数 求ya2w w,f,乃 0x 0x0z 解:令u=x+y+z,v=xyz,则 w=f(u,v) 8=1+户 x y Zx y Z =(x+y+2,xy2)+y2f5(x+y+,xy2 0x02 =1+xy+y+yz[f1+xy] =i+(x+z)2+xy2f2+y3 HIGH EDUCATION PRESS 机动目录上页下页返回结束
为简便起见 , 引入记号 , , 2 1 12 u v f f u f f = = 例5. 设 f 具有二阶连续偏导数, 求 , . 2 x z w x w 解: 令 u = x + y + z , v = xyz, x w w u v x y z x y z w = f (u, v) + f yz 2 ( , ) 2 + y z f x + y + z xyz 则 x z w 2 22 2 2 11 12 = f + y(x + z) f + xy z f + y f + f xy 12 + f x y 221 2 , f , f 机动 目录 上页 下页 返回 结束

主观题10分 ⊙设置 3.设三=f(2x-y,ysinx)),其中f(u,v)有二阶连 续偏导数,求d:az ax'⑦ 正常使用主观题需2.0以上版本雨课堂 HIGH EDUCATION PRESS 作答
3.设 其中 有二阶连 续偏导数,求 作答 正常使用主观题需2.0以上版本雨课堂 z f x y y x = − (2 , sin ), f u v ( , ) , z z x y 主观题 10分