
说明: 若定理中f(u,v)在点(u,y)偏导数连续减弱为 偏导数存在,则定理结论不一定成立 u v 例如:2=f(4,)= 2+22+20 0 u2+v2=0 u=t,v=t 易知 (0000=0,g 6z (0,0)=/(0,0)=0 但复合函数:=j化,0-号 dz 1 Oz du.Oz dv dt 2 ou dt Ov dt =01+01=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束
说明: 若定理中 例如: z = f (u, v) = u = t , v = t 易知: 但复合函数 z = f (t, t) 2 1 d d = t z t v v z t u u z d d d d + = 01+ 01= 0 偏导数连续减弱为 偏导数存在, 2 t = , 0 2 2 2 2 2 + + u v u v u v 0 , 0 2 2 u + v = 机动 目录 上页 下页 返回 结束 则定理结论不一定成立

推广:设下面所涉及的函数都可微 1)中间变量多于两个的情形.例如,z=f(u,v,1w), u=p(t),V=W(t),w=0(t) dz 0z du Oz dv 0z dw dt Ou di Ov dt'ow dt =f0'+5w+f分o 2)中间变量是多元函数的情形例如, z=f(u,v),u=o(x,y),v=V(x,y) a正a2.u+5.=m+ 8x Ou Ox Bv 8x 0z Oz Ou.Oz.Ov =p3+f3w3 ay Ou ay'Ov Oy HIGH EDUCATION PRESS 机动目录上页下页返回结束
推广: 1) 中间变量多于两个的情形. 例如, z = f (u,v,w) , 设下面所涉及的函数都可微 . = t z d d = + + 1 2 3 f f f 2) 中间变量是多元函数的情形.例如, z = f (u,v) , u = (x, y), v = (x, y) = x z 11 21 = f + f 1 2 2 2 = = f + f y z z z u v w u v x y x y t t t t u u z d d t v v z d d + t w w z d d + x u u z x v v z + y u u z y v v z + 机动 目录 上页 下页 返回 结束 u = (t), v = (t), w = (t)

又如,z=f(x,y),v=W(x,y) 当它们都具有可微条件时,有 of bv 8x Ox Bv Ox =+乃 0z of bv Ov =52 注意: 这里 与1不同 8x 表示固定y对x求导, of 8x 表示固定v对x求导 口诀:分段用乘,分叉用加,单路全导,叉路偏导 HIGH EDUCATION PRESS 机动目录上页下页返回结束
又如, z = f (x,v), v = (x, y) 当它们都具有可微条件时, 有 x z 1 21 = f + f y z 2 2 = f z = f x x y 注意: 这里 x z x f x z 表示固定 y 对 x 求导, x f 表示固定 v 对 x 求导 口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏导 x f = 与 不同, v 机动 目录 上页 下页 返回 结束

例2.设z=e“sinv,u=xy,v=x+y,求 Da 0z Ox'Oy 解: 0z0z Ou 0z Ov Ox -Ou Ox "Ov Ox =e“sinv.y+e“cosv.l =e*[y.sin(x+y)+cos(x+)] 8z Oz Bu,8z Ov 1 0y Ou ay'Ov Oy e"sinv .x +e"cosv .1 =ex[x.sin(x+y)+cos(x+y)] HIGH EDUCATION PRESS ◆0C08 机动目录上页下页返回结束
例2. 设 z e sin v, u xy , v x y , u = = = + , . y z x z 求 解: x z e v u = sin y z e v u = sin x v v z + e v u + cos y v v z + e v u + cos 1 1 z u v x y x y 机动 目录 上页 下页 返回 结束
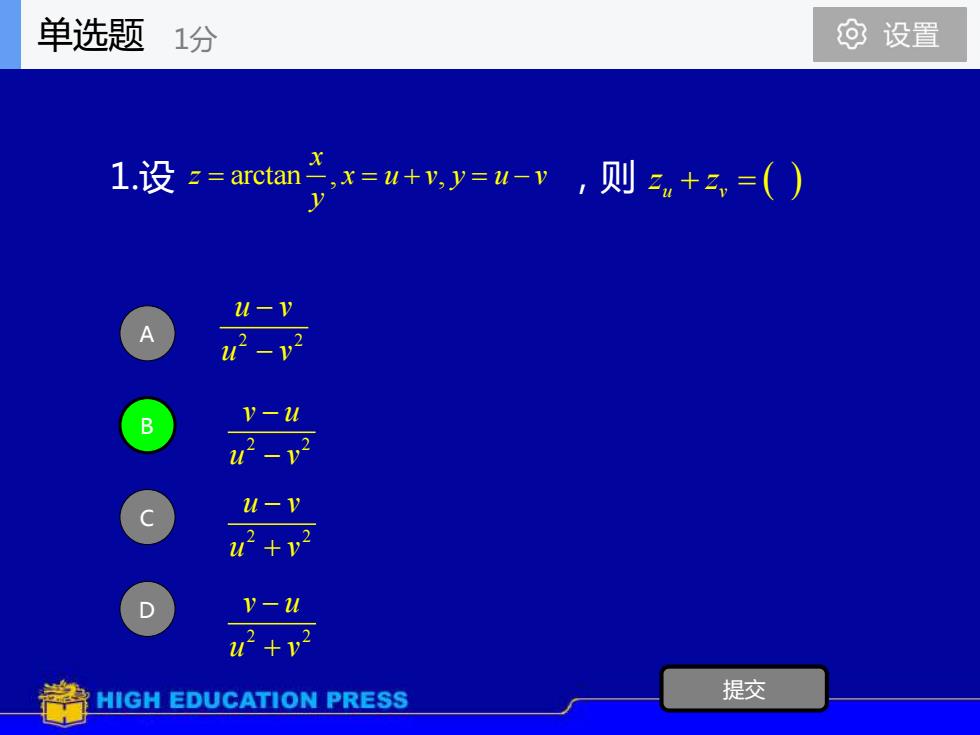
单选题 1分 ⊙设置 X 1.设z=arctan,x=u+y,y=u-v,则z,+,=() 2 u-v w-v V-u 7-v u-y +y v-u + HIGH EDUCATION PRESS 提交
1.设 ,则 A B C D 提交 arctan , , x z x u v y u v y = = + = − z z u v + = ( ) 2 2 u v u v − − 2 2 v u u v − − 2 2 u v u v − + 2 2 v u u v − + 单选题 1分