
凸集---凸锥(Convex Cone〉 定义锥、凸锥 设S三R”,x。∈S,如果对一切∈S 及2>0,有x。+2x∈S,则称S是 以x为顶点的锥如果S又是凸集, 则称S为凸维
定义 锥、凸锥 S . x . S 0, x x S, S , x S 0 0 0 则 称 为凸锥 以 为顶点的锥 如 果 又是凸集, 及 有 则 称 是 设 ,如果对一切 + S R x S n 凸集-----凸锥 (Convex Cone)

凸函数 凸函数(Convex Function)--定义2.4 设D≤R”是非空凸集,f(x):S→R, 若对任意的x,Jy∈D,及任意的a∈[0,1] 都有(ax+1-a)y)≤af(x)+(1-a)f(y) 则称函数f(x)为D上的凸函数 注:将上述定义中的不等式反向,可以得到 凹函数的定义
凸函数 凸函数(Convex Function) ----定义2.4 设 是非空凸集, f (x): S → R, n D R 若对任意的 x, y D, 及任意的 0,1 都有: f (x + (1−)y) f (x)+ (1−)f (y) 则称函数 f (x) 为 D 上的凸函数. 注:将上述定义中的不等式反向,可以得到 凹函数的定义.

凸函数 严格凸函数 设D三R” 是非空凸集,f(x):S→R, 若对任意的x,y∈D(x≠y),及任意的a∈(O,1) 都有:f(cx+(1-a))<f(x)+(1-a)f(y) 则称函数.f(x)为D 上的严格凸函数 注:将上述定义中的不等式反向,可以 得到严格凹函数的定义
凸函数 严格凸函数 设 是非空凸集, f (x): S → R, n D R 若对任意的 x y D x y , ( ), 及任意的 (0,1) 都有: f x y f x f y ( + − + − (1 1 ) ) ( ) ( ) ( ) 则称函数 f (x) 为 D 上的严格凸函数. 注:将上述定义中的不等式反向,可以 得到严格凹函数的定义.

凸函数 几何性质 对一元函数f(x),在几何上f(x,)+(1-a)f(x2 0≤≤1)表示连接(x1,f(x),(x2,f(x2)的线段 ·f(a,+(1-a)x,)表示在点ax,+(-a)x,处的 函数值 所以一元凸函数表示连接函数图形上任意两点 的线段总是位于曲线弧的上方
凸函数 ⚫ 对一元函数 f (x), 在几何上 ( ) ( ) ( ) 1 1 x2 f x + − f (0 1) 表示连接 ( ( )) ( ( )) 1 1 2 2 x , f x , x , f x 的线段. 所以一元凸函数表示连接函数图形上任意两点 的线段总是位于曲线弧的上方. 几何性质 ( ( ) ) x1 1 x2 f + − 表示在点 ( ) x1 + 1− x2 处的 函数值. ⚫
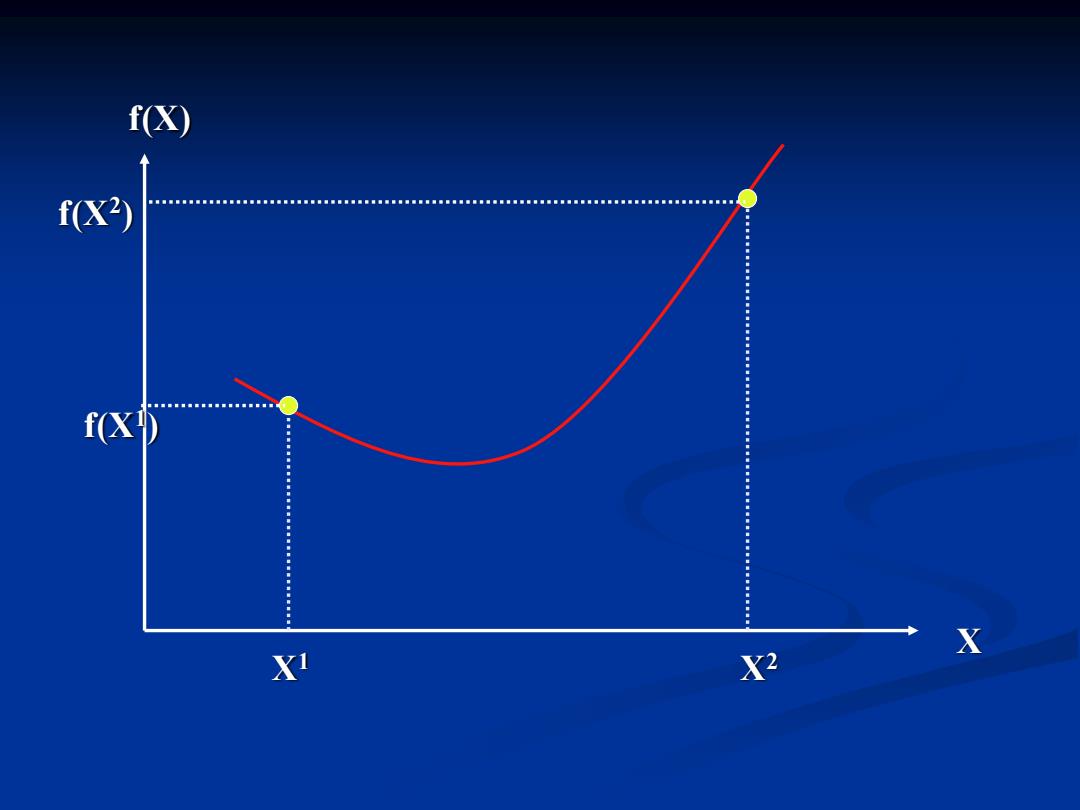
f(X) f(X2) fX) X X X2
f(X) X f(X 1 ) f(X 2 ) X 1 X 2