焦点的位置 焦点在x轴上 焦点在y轴上 顶点 (0,±0) 轴长 虚轴长=,实轴长= 焦点 F1(-c,0),F2(c,0) 焦距 对称性 对称轴为 ,对称中心为 离心率 渐近线 后±(或 (或y=±x)
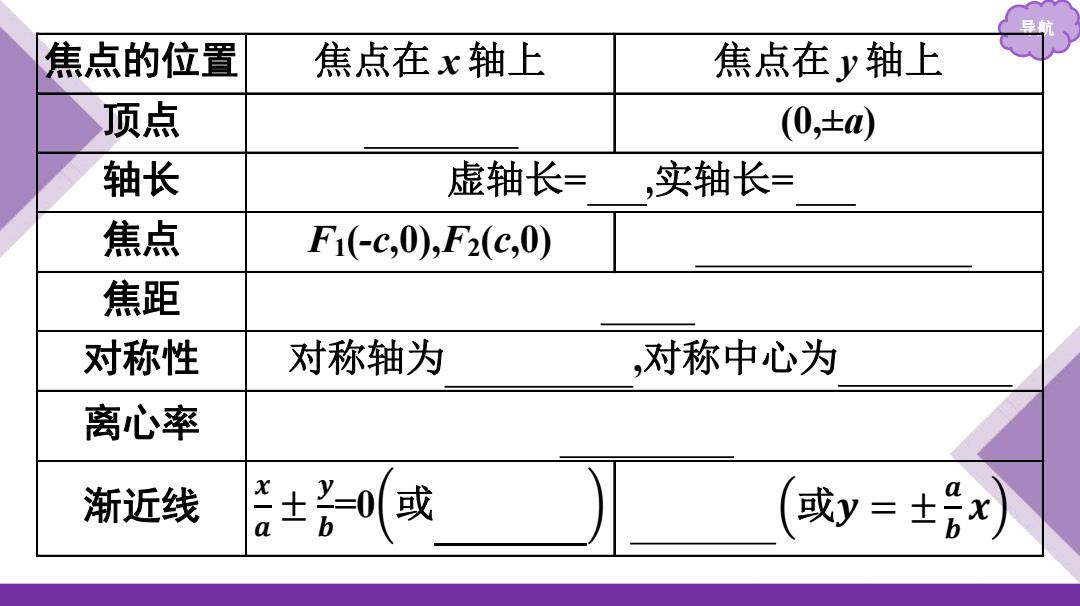
导航 焦点的位置 焦点在 x 轴上 焦点在 y 轴上 顶点 (±a,0) (0,±a) 轴长 虚轴长= 2b ,实轴长= 2a 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c) 焦距 2c 对称性 对称轴为 x 轴、y 轴 ,对称中心为 原点(0,0) 离心率 e= 𝐜 𝐚 (e>1) 渐近线 𝒙 𝒂 ± 𝒚 𝒃 =0 或𝐲 = ± 𝒃 𝒂 𝒙 𝒚 𝒂 ± 𝒙 𝒃 =0 或𝒚 = ± 𝒂 𝒃 𝒙

导 3.做一做:已知双曲线16x29y2=-144,试求双曲线的半实轴长、 半虚轴长、焦点坐标、顶点坐标、离心率 解:方程可化为若-号1,则a4,635, 故半实轴长为4,半虚轴长为3,焦点坐标为(0,5),(0,-5),顶点坐 标为0,4,0,-4),离心率
导航 3.做一做:已知双曲线16x 2 -9y 2=-144,试求双曲线的半实轴长、 半虚轴长、焦点坐标、顶点坐标、离心率. 解:方程可化为𝒚 𝟐 𝟏𝟔 − 𝒙 𝟐 𝟗 =1,则 a=4,b=3,c=5, 故半实轴长为 4,半虚轴长为 3,焦点坐标为(0,5),(0,-5),顶点坐 标为(0,4),(0,-4),离心率 e= 𝟓 𝟒

导航 【思考辨析】 判断正误(正确的画“V,错误的画“义) (④双曲线方程器一二1a00中的x的取值范围为 (-o0,-dU[4,+oo).( (2)双曲线在无穷远处可与渐近线相交.( (3)双曲线的实轴比虚轴长( (4)双曲线的离心率e的取值范围为(0,1).(
导航 【思考辨析】 判断正误.(正确的画“√”,错误的画“×”) (1)双曲线方程 (a>0,b>0)中的x的取值范围为 (-∞,-a]∪[a,+∞).( √ ) (2)双曲线在无穷远处可与渐近线相交.( × ) (3)双曲线的实轴比虚轴长.( × ) (4)双曲线的离心率e的取值范围为(0,1).( × ) 𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃 𝟐 =1

导航、 课堂·重难突破 探究一双曲线的几何性质 【例1】求双曲线9y24x2=-36的顶点坐标、焦点坐标、实轴 长、虚轴长、离心率和渐近线方程
导航 课堂·重难突破 探究一 双曲线的几何性质 【例1】求双曲线9y 2 -4x 2=-36的顶点坐标、焦点坐标、实轴 长、虚轴长、离心率和渐近线方程

导航 解:将9242-36化为号- 则=3,b=2,c=V13, 故顶点坐标为(-3,0),(3,0), 焦点坐标为(V13,0),(V13,0), 实轴长为2=6,虚轴长为2b=4, 离心率=零,浙近线方程为之=导
导航 解:将 9y 2 -4x 2 =-36 化为𝒙 𝟐 𝟗 − 𝒚 𝟐 𝟒 =1, 则 a=3,b=2,c=√𝟏𝟑, 故顶点坐标为(-3,0),(3,0), 焦点坐标为(-√𝟏𝟑,0),(√𝟏𝟑,0), 实轴长为 2a=6,虚轴长为 2b=4, 离心率 e= 𝒄 𝒂 = √𝟏𝟑 𝟑 ,渐近线方程为 y=± 𝒃 𝒂 x=± 𝟐 𝟑 x