《高等数学》课程教学资源（PPT课件）第十章_D10_2二重积分的计算

例4.求(x2+y)dc,其中D是由抛物线 D y=x2和x=y2所围平面闭区域， 解：画积分区域 1.2 = 两曲线的交点 0. 0.6 0. 0. 0.20.40.60.8 1 D:0≤x≤1，x2≤y≤x (x+)=(x2+y =[x-x)+j(x-x) .33 140 HIGH EDUCATION PRESS

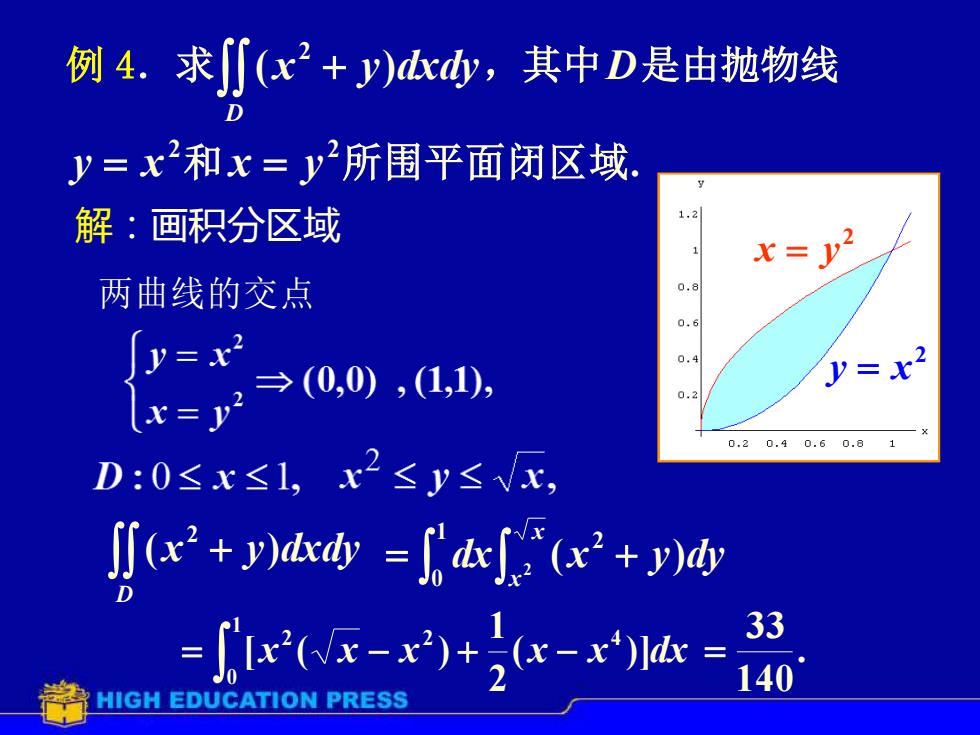
例 4．求 + D (x y)dxdy 2 ，其中D是由抛物线 解：画积分区域 两曲线的交点  + D ( x y)dxdy 2   = + 1 0 2 2 ( ) x x dx x y dy x x x ( x x )]d x 2 1 [ ( ) 2 4 1 0 2 = − + −  . 140 33 = 2 y = x 2 x = y 2 y = x 2 x = y 2 y = x 和 2 x = y 所围平面闭区域

小结（二重积分计算） 1.计算二重积分的步骤 (1)画出积分区域D的草图. (2)用不等式组表示积分区域D(X型或Y型) (3)把二重积分表示为二次积分（也称累次积分）： 如果D是X型区域：a≤x≤b,px)p(x),则 ady=xw. D >如果D是Y型区域：c凶d,yy)x≤y),则 jfx,drdy=dyfx,dx D (4)计算二次积分 HIGH EDUCATION PRESS

   = b a x x D f x y d d x f x y d y ( ) ( ) 2 1 ( , ) ( , )    . ➢ 如果D是X型区域: axb, 1 (x)y2 (x), 则 1.计算二重积分的步骤 ➢ 如果D是Y型区域: cyd, 1 (y)x2 (y), 则 (1)画出积分区域D的草图. (2)用不等式组表示积分区域D ( X 型或 Y 型). (3)把二重积分表示为二次积分（也称累次积分）: (4)计算二次积分. 2 1 ( ) ( ) ( , ) d y y f x y x   d d c y   D f ( x, y) d x d y ☺ 小结（二重积分计算）

2.若积分区域既是X-型区域又是Y-型区域， 则有∬nfx,)dxd dy 为计算方便，可选择积分序 必要时还可以交换积分序 =ayxa 如果D是X型区域：a≤x≤b,p(x)Sy≤P(x),则 I,axdy=g/4 如果D是Y型区域：cy≤d,yy)sx≤4y),则 rc,ddydyfk,ar HIGH EDUCATION PRESS

   = b a x x D f x y d d x f x y d y ( ) ( ) 2 1 ( , ) ( , )    . ➢ 如果D是X型区域: axb, 1 (x)y2 (x), 则 ➢ 如果D是Y型区域: cyd, 1 (y)x2 (y), 则 2 1 ( ) ( ) ( , ) d y y f x y x   d d c y   D f ( x, y) d x d y 2. 若积分区域既是X–型区域又是Y –型区域 , D 则有 f (x, y)dx dy f x y y x x ( , )d ( ) ( ) 2 1     = b a d x f x y x y y ( , )d ( ) ( ) 2 1     = d c d y 为计算方便,可选择积分序, 必要时还可以交换积分序