《线性代数》课程教学资源（PPT课件）第三章 矩阵的初等变换及线性方程组 3.1 矩阵的初等变换

如果矩阵A经有限次初等变换变矩阵B, 就称矩阵A与B等价，记作A~B. 等价矩阵的性质： (1)反身性A~A; (2)对称性若A~B,则B~4 (3)传递性若A~B,B~C,则A~C

就称矩阵 与 等价，记作 ． 如果矩阵 经有限次初等变换变成矩 阵 ， A B A B A B ~ 等价矩阵的性质: （１）反身性 A A  ； （２）对称性 若 , A B B A   则 ; （３）传递性 若 , A B B C A C    ,则 ;

用矩阵的初等行变换解方程组(1)： 2-1-1 12 1 1-2 1-4 B= 4-6 2-2 4 3 6 -9 7 9 1 1 -2 1 i←今2 2 -1 -1 12 =B1 3÷2 2 -3 1 -1 2 3 6-9 7 9)

用矩阵的初等行变换 解方程组（1）：               − − − − − − − = 3 6 9 7 9 4 6 2 2 4 1 1 2 1 4 2 1 1 1 2 B 1 3 6 9 7 9 2 3 1 1 2 2 1 1 1 2 1 1 2 1 4 = B               − − − − − − 1 2 r  r r3  2

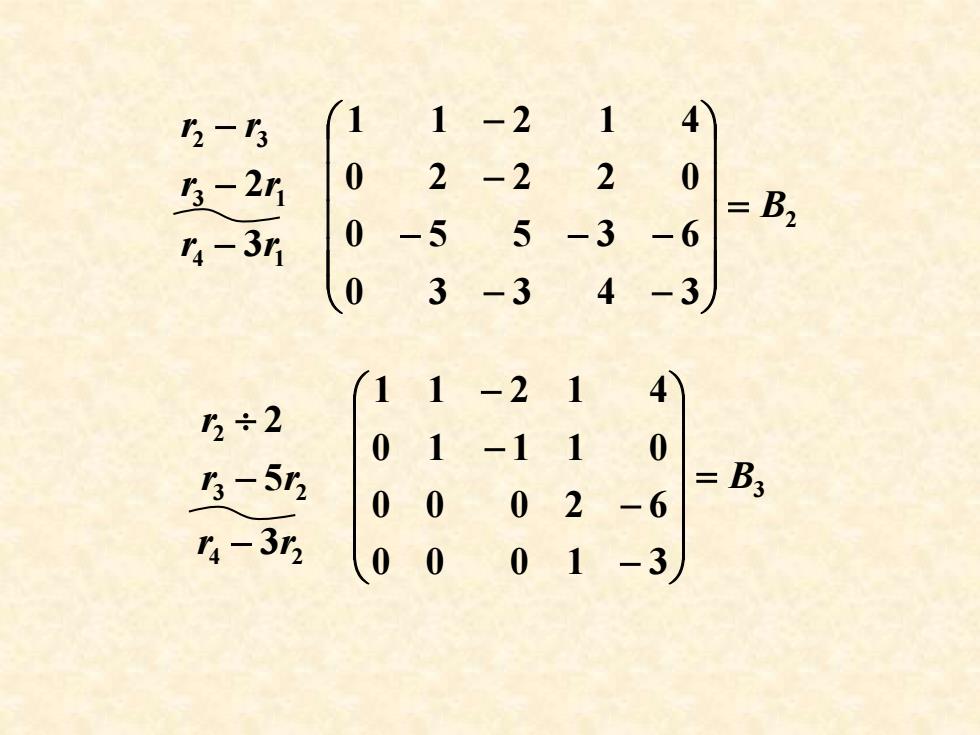
3-3 1 1-2 1 4 3-2r 0 2-2 2 0 0-5 5-3 =B2 4-3 -6 03-3 4-3 11 -2 1 4 2÷2 01 -1 10 3-5 =B3 00 02 -6 4-33 00 01 -3

3 0 0 0 1 3 0 0 0 2 6 0 1 1 1 0 1 1 2 1 4 = B               − − − − 2 0 3 3 4 3 0 5 5 3 6 0 2 2 2 0 1 1 2 1 4 = B               − − − − − − − 3 1 2 3 r 2r r r − − 4 3 1 r − r 3 2 2 5 2 r r r −  4 3 2 r − r