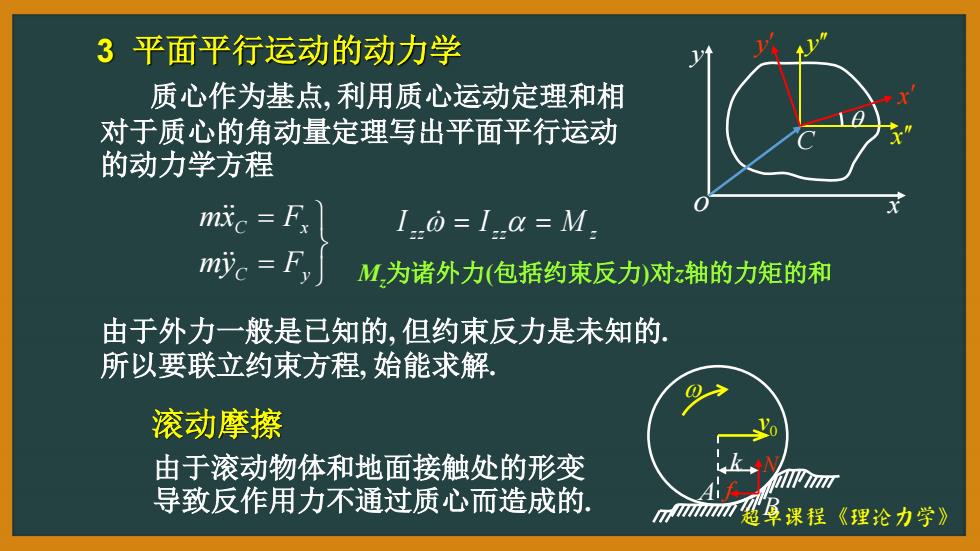
3平面平行运动的动力学 质心作为基点,利用质心运动定理和相 对于质心的角动量定理写出平面平行运动 的动力学方程 m成e=Fx I:0=I.a=M. myc F, M,为诸外力(包括约束反力)对z轴的力矩的和 由于外力一般是已知的,但约束反力是未知的 所以要联立约束方程,始能求解, 0 滚动摩擦 由于滚动物体和地面接触处的形变 导致反作用力不通过质心而造成的. 孕课程《理论力学》
超卓课程《理论力学》 3 平面平行运动的动力学 质心作为基点, 利用质心运动定理和相 对于质心的角动量定理写出平面平行运动 的动力学方程 C y C x my F mx F z z z z M z I I Mz为诸外力(包括约束反力)对z轴的力矩的和 由于外力一般是已知的, 但约束反力是未知的. 所以要联立约束方程, 始能求解. 滚动摩擦 由于滚动物体和地面接触处的形变 导致反作用力不通过质心而造成的. x y o C x x y y f k N A B 0 v

例:设椭圆规尺AB的端点A和B沿直线导槽Ox及Oy滑V 动,而B以匀速度c运动。用转动瞬心法求规尺上M点 的速度、加速度,并求本体极迹和空间极迹的方程式。B 解:过A,B分别作,和V的垂线,则两条直线的交点 C就是瞬心. .'v=c=@CB=@(a+b)sin0 1 ∴.0= a+b sin0 M点的速度:y-oC7=,Gsr0+co0-b+bewF0 以B为基点,M点的加速度为:a=。+d0x-o7 do dt 超卓课程《理论力学》
超卓课程《理论力学》 例:设椭圆规尺AB的端点A和B沿直线导槽Ox 及Oy 滑 动,而B以匀速度c 运动。用转动瞬心法求规尺上M点 的速度、加速度,并求本体极迹和空间极迹的方程式。 解:过A,B分别作 和 的垂线, 则两条直线的交点 C就是瞬心 . M点的速度: 以B为基点, M点的加速度为: