直接积分法 被积函数进行恒等变形,使用基本积分表计算不 定积分的方法 (凑微分法) 第一类换元法 ∫f八p(x)p'(x)c=可f(o)dw=px 换元积分法 第二类换元法 jfenwowual 三角代换、倒代换、根式代换 类方分不 金资鞋嶺 分部积分法 分部积分公式 ∫uw=w-∫wa 有理函数的积分 将有理函数化为部分分式之和的积分 特殊类型函 三角函数有理式的积分 万能置换公式 数的积分法 简单无理函数的积分 R(x,R/ax+B),R(x, 解决方法作代换去掉根号. 令t=/a+b;令t= ax+b cx+e D程学院
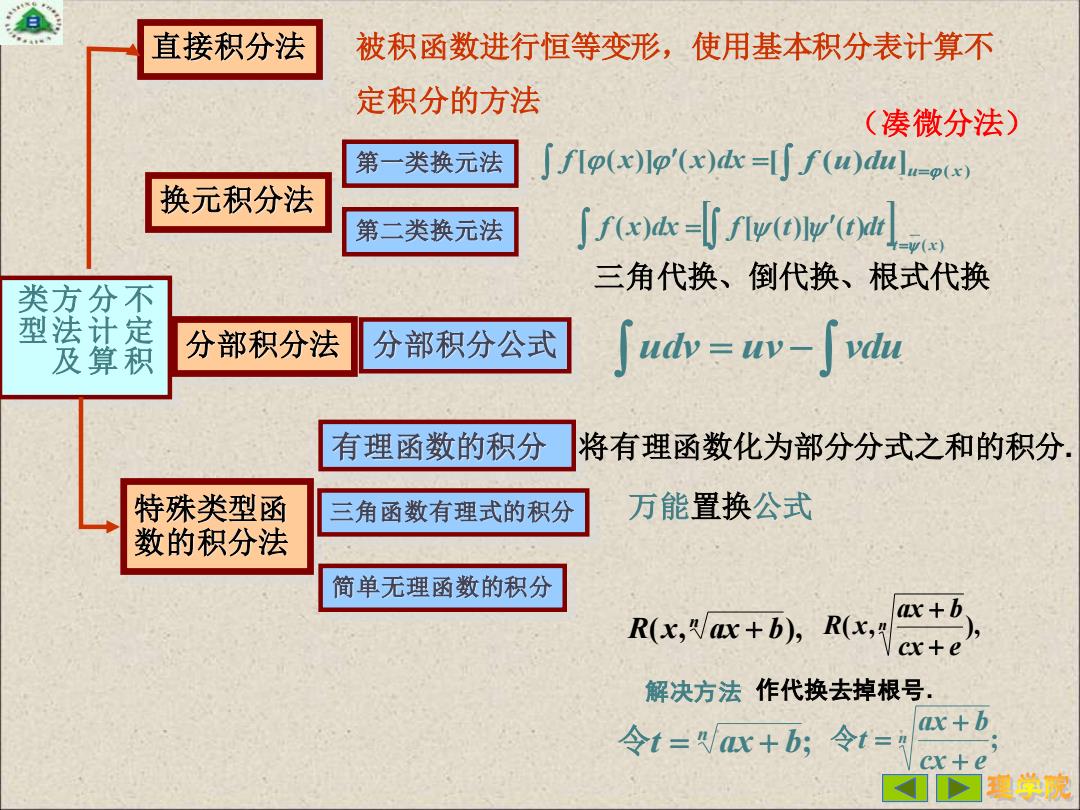
不 定 积 分 计 算 方 法 及 类 型 直接积分法 被积函数进行恒等变形,使用基本积分表计算不 定积分的方法 换元积分法 第一类换元法 f[(x)](x)dx = = ( ) [ ( ) ] u du u x f 第二类换元法 ( ) ( ) [ ( )] ( ) t x f x dx f t t dt = = 分部积分法 udv uv vdu 分部积分公式 = − 特殊类型函 数的积分法 有理函数的积分 将有理函数化为部分分式之和的积分. 三角函数有理式的积分 简单无理函数的积分 ( , ), n R x ax + b ( , ), n cx e ax b R x + + 解决方法 作代换去掉根号. 万能置换公式 ; n 令t = ax + b ; n cx e ax b t + + 令 = 三角代换、倒代换、根式代换 (凑微分法)

定积分 一、概念、性质、几何意义 二、计算: 牛顿一莱布尼兹公式: [f(x)dx=F(b)-F(a) F'(x)=f(x) 换元积分公式:心fx)=f1o(0o'm)dh 分部积分公式: udw=[wmlg-心vda >习程学院
定积分 一、概念、性质、几何意义 二、计算: 牛顿—莱布尼兹公式: f (x)d x F(b) F(a) F'(x) f (x) b a = − = 换元积分公式: = f x d x f t t dt b a ( ) [ ( )] '( ) 分部积分公式: = − b a b a b a udv [uv] vdu

三、利用定积分换元法证明积分等式 四、关于积分上限函数的问题 设f(x)eC[a,b],Φ(x)=ft)d,则 1. Φ'(x)=f(x) 2. ud=-n 3. id()0 4. f0d)-u咖-j小w ID可程学院
三、利用定积分换元法证明积分等式 四、关于积分上限函数的问题 设 = x a f (x) C[a,b], (x) f (t)d t ,则 ( ) ( ) 1. ( ) ( ) 2. ( ( ) ) ( ) 3. lim ( ) ( ) 0 4. ( ( ) ) [ ( )] '( ) [ ( )] '( ) b x x x a a u x v x x f x d f x dx f x dx f t dt a d f t dt f u x u x f v x v x dx → = = − = = = −

注意特殊形式的定积分计算 1.对称区间上的积分 考察被积函数是否为奇偶函数,用奇偶函数 的“特性”处理 2.分段函数的积分 认清积分限是被积函数定义域的哪个区间 的端点,然后按段积分求和 >可程学院
特殊形式的定积分计算 1. 对称区间上的积分 考察被积函数是否为奇偶函数, 注意 用奇偶函数 的“特性”处理 .2. 分段函数的积分 认清积分限是被积函数定义域的哪个区间 的端点,然后按段积分求和

3.被积函数带有绝对值符号的积分 在作积分运算之前设法去掉绝对值.(注意符号) 4.被积函数中含有“积分上限的函数”的积分 用分部积分法做,将积分上限的函数取作. 个少程学院
3. 被积函数带有绝对值符号的积分 在作积分运算之前设法去掉绝对值.(注意符号!) 4. 被积函数中含有“积分上限的函数”的积分 用分部积分法做,将积分上限的函数取作u