
离散数学 第十三章几种特殊的图 主要内容 ●欧拉图 ●1 哈密顿图 ●二部图与匹配 平面图 ●着色 1
1 第十三章 几种特殊的图 主要内容 ⚫ 欧拉图 ⚫ 哈密顿图 ⚫ 二部图与匹配 ⚫ 平面图 ⚫ 着色

离散数学 13. 1欧拉图 历史背景:哥尼斯堡七桥问题 B A B D 2
2 13.1 欧拉图 历史背景:哥尼斯堡七桥问题

离散数学 欧拉图定义 定义13.1图(无向图或有向图)中所有边恰好通过一次且经过 所有顶点的通路称为欧拉通路.图中所有边恰好通过一次且 经过所有顶点的回路称为欧拉回路.具有欧拉回路的图称为 欧拉图.具有欧拉通路而无欧拉回路的图称为半欧拉图. 说明: 规定平凡图为欧拉图. 环不影响图的欧拉性 3
3 欧拉图定义 定义13.1 图(无向图或有向图)中所有边恰好通过一次且经过 所有顶点的通路称为欧拉通路. 图中所有边恰好通过一次且 经过所有顶点的回路称为欧拉回路.具有欧拉回路的图称为 欧拉图. 具有欧拉通路而无欧拉回路的图称为半欧拉图. 说明: 规定平凡图为欧拉图. 环不影响图的欧拉性
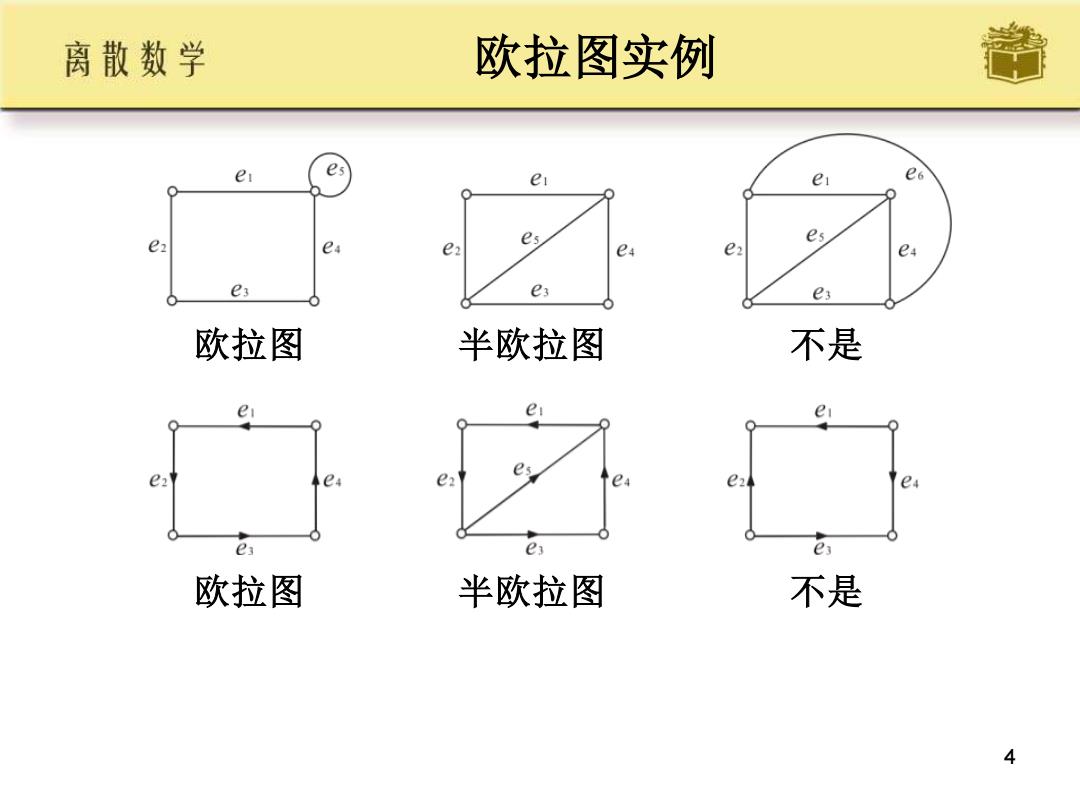
离散数学 欧拉图实例 er es er es e es e es e e e es e, es 欧拉图 半欧拉图 不是 e ei e es e; e, e, 欧拉图 半欧拉图 不是 4
4 欧拉图实例 欧拉图 半欧拉图 不是 欧拉图 半欧拉图 不是

离散数学 欧拉图的判别法 定理13.1(1)无向图G是欧拉图当且仅当G是连通的且没有奇 度顶点 (2)无向图G是半欧拉图当且仅当G是连通的且恰有两个奇度 顶点 (3)有向图D是欧拉图当且仅当D是强连通的且每个顶点的入 度等于出度. (4)有向图D是半欧拉图当且仅当D是单向连通的且恰有两个 奇度顶点,其中一个顶点的入度比出度大1,另一个顶点出度 比入度大1,其余顶点的入度等于出度. 例1设G是非平凡的欧拉图,则G≥2. 证只需证明G的任意一条边都不是桥.设C是一条欧拉回路, e在C上,因而G-e仍是连通的,故e不是桥. 5
5 欧拉图的判别法 定理13.1 (1) 无向图G是欧拉图当且仅当G是连通的且没有奇 度顶点. (2) 无向图G是半欧拉图当且仅当G是连通的且恰有两个奇度 顶点. (3) 有向图D是欧拉图当且仅当D是强连通的且每个顶点的入 度等于出度. (4) 有向图D是半欧拉图当且仅当D是单向连通的且恰有两个 奇度顶点, 其中一个顶点的入度比出度大1, 另一个顶点出度 比入度大1, 其余顶点的入度等于出度. 例1 设G是非平凡的欧拉图,则(G)2. 证 只需证明G的任意一条边e都不是桥. 设C是一条欧拉回路, e在C上,因而G−e仍是连通的,故e不是桥.