
导数在求极限中的应用-一洛比达法则 0型及°型(0.0,0-0,0°,1,0型) ∞ 洛必达法则 lim f( _Im f'(x) x-→aF(x -→a F'(x) >可程学院
型及 型 0 0 (0 , ,0 ,1 , ) − 0 0 型 洛必达法则 ( ) ( ) lim ( ) ( ) lim F x f x F x f x x a x a = → → 方 法 导数在求极限中的应用---洛比达法则
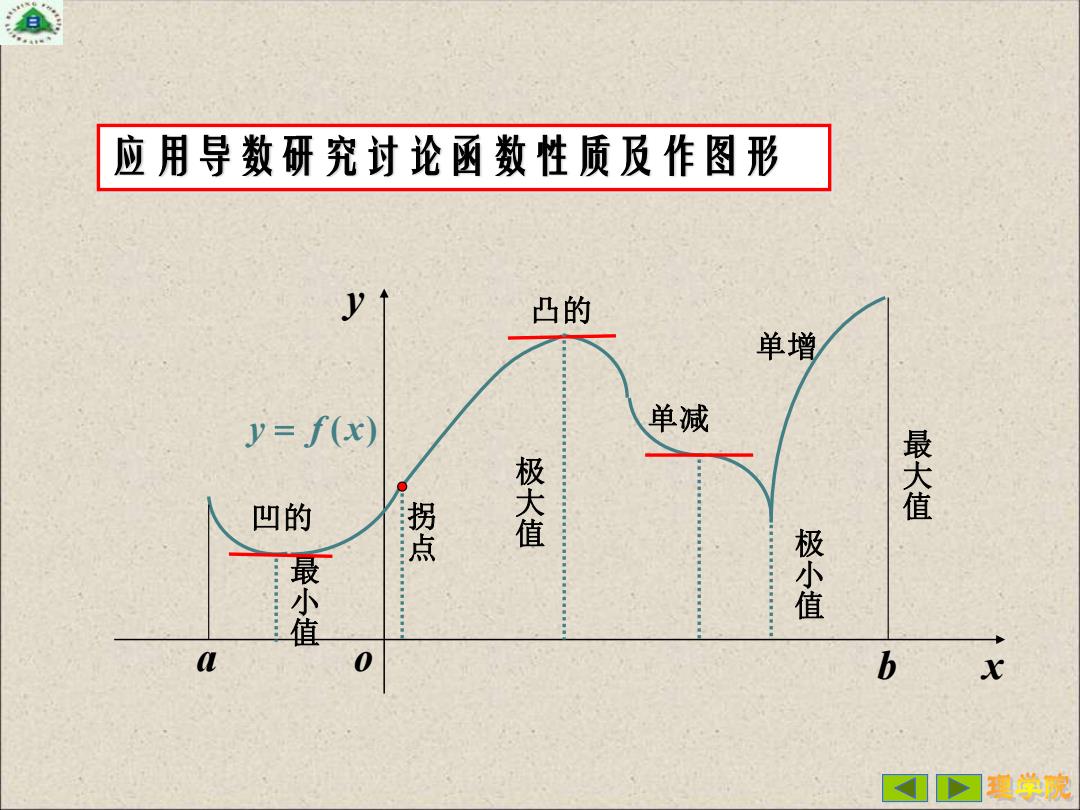
应用导数研究讨论函数性质及作图形 y 凸的 单增 y=f(x) 单减 极大值 最大值 凹的 程 最小值 极小值 L 0 b x ①>习程学院
x y a o b 最 大 值 最 小 值 极 大 值 极 小 值 拐 点 凹的 凸的 单增 y = f (x) 单减 应用导数研究讨论函数性质及作图形
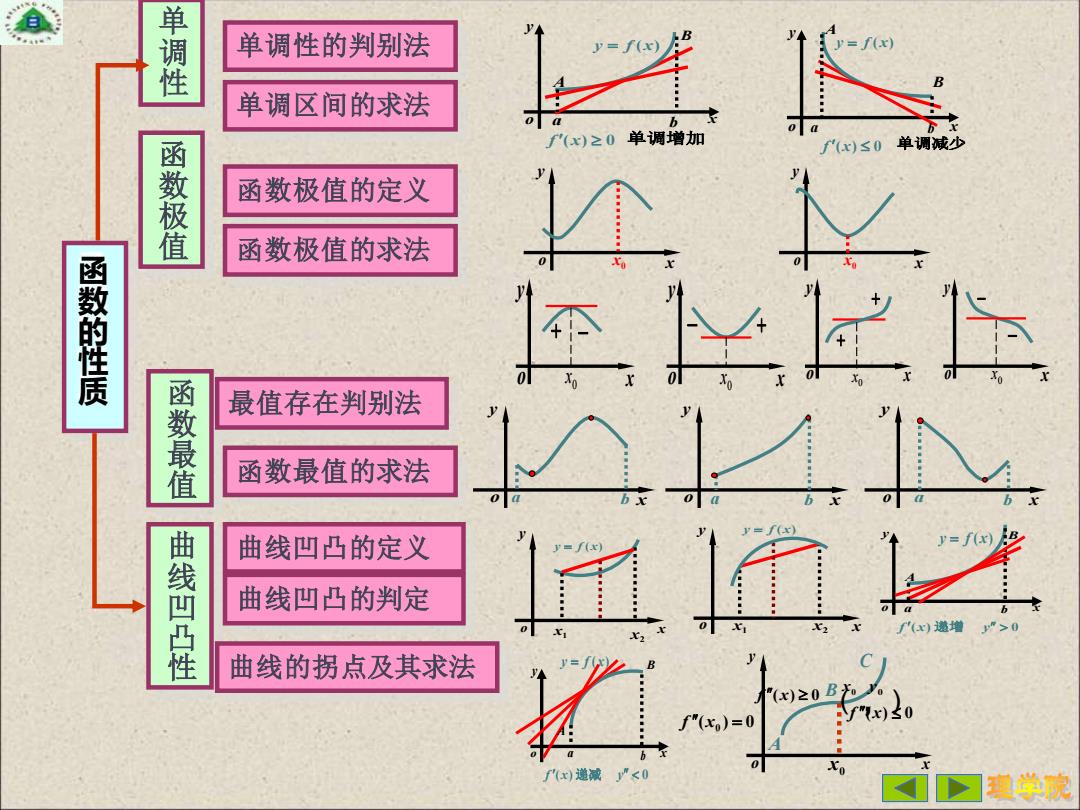
单调性 单调性的判别法 y=f(x) 单调区间的求法 b f(x)≥0单调增加 f(x)≤0单调减少 函数极值 函数极值的定义 函数极值的求法 函数的性质 函数最值 最值存在判别法 函数最值的求法 ☑ 曲线凹凸的定义 曲线凹凸性 曲线凹凸的判定 (ax)增 曲线的拐点及其求法 f'x)递减y"<0 D程学院
函数的性质 单调性 单调性的判别法 x yo y = f (x ) a b A B f (x) 0 单调增加 x yo y = f (x) f (x) 0 a bB A 单调减少 单调区间的求法 函数极值 函数极值的定义 函数极值的求法 o x y x0 o x y 0 x x yo x y x0 o 0 x + − − + x yo x yo 0 x 0 x + − − + 函数最值 最值存在判别法 o x y o x y a b o x y a b a b 函数最值的求法 曲线凹凸性 曲线凹凸的定义 曲线凹凸的判定 曲线的拐点及其求法 x yo y = f (x ) x 1 x 2 x yo x1 x2 y = f (x ) x yo y = f (x ) a b A B f (x) 递增 y 0 x yo y = f (x) a bB A f (x) 递减 y 0 f (x0 ) = 0 x yo A B C x0 0 y x0 ( , ) f ( x ) 0 f ( x ) 0
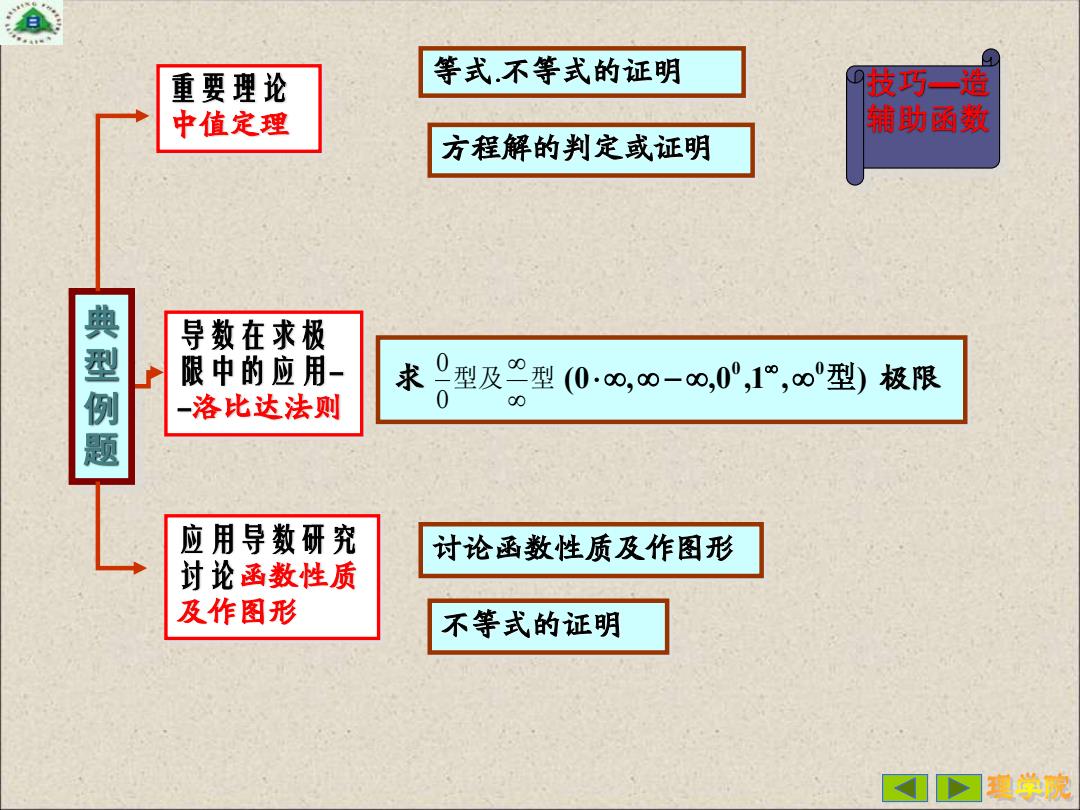
重要理论 等式不等式的证明 技巧一造 中值定理 辅助函数 方程解的判定或证明 典型例题 导数在求极 限中的应用- 求0型及型(00,0-0,0°,1,60型)极限 -洛比达法则 0 应用导数研究 讨论函数性质及作图形 讨论函数性质 及作图形 不等式的证明 ①>习程学院
典 型 例 题 重要理论 中值定理 导数在求极 限中的应用- -洛比达法则 应用导数研究 讨论函数性质 及作图形 等式.不等式的证明 方程解的判定或证明 型及 型 0 0 (0 , ,0 ,1 , ) 求 − 0 0型 极限 讨论函数性质及作图形 不等式的证明 技巧—造 辅助函数

原函数 F(x)=f(x)dF(x)=f(x)dx 不定积分的概念 原函数存在定理 连续函数一定有原函数, 不定积分的定义 函数f(x)的带有任意常数项的原函数 不定积分的概念与性质 称为f(x)在区间I内的 不定积分,记为f(x)=F(x)+C 基本积分表 不定积分的性质 (1) jf(x)±gx=fx)±∫g(x)ac; (此性质可推广到有限多个函数之和的情况) (2)∫fx)=k∫f(x)k.(k是常数,k≠0) >习程学院
不 定 积 分 的 概 念 与 性 质 不 定 积 分 的 概 念 原函数 F(x) = f (x) 或 dF x f x dx ( ) ( ) = 原函数存在定理 连续函数一定有原函数. 不定积分的定义 函数 f (x)的带有任意 常数项的原函数 称为 f (x)在区间I内的 不定积分,记为 f (x)dx.= + F x C ( ) 不 基本积分表 定 积 分 的 性 质 (1) [ f (x) g(x)]dx = ( ) ( ) ; f x dx g x dx (此性质可推广到有限多个函数之和的情况) (2) kf (x)dx = ( ) . k f x dx (k是常数,k 0)