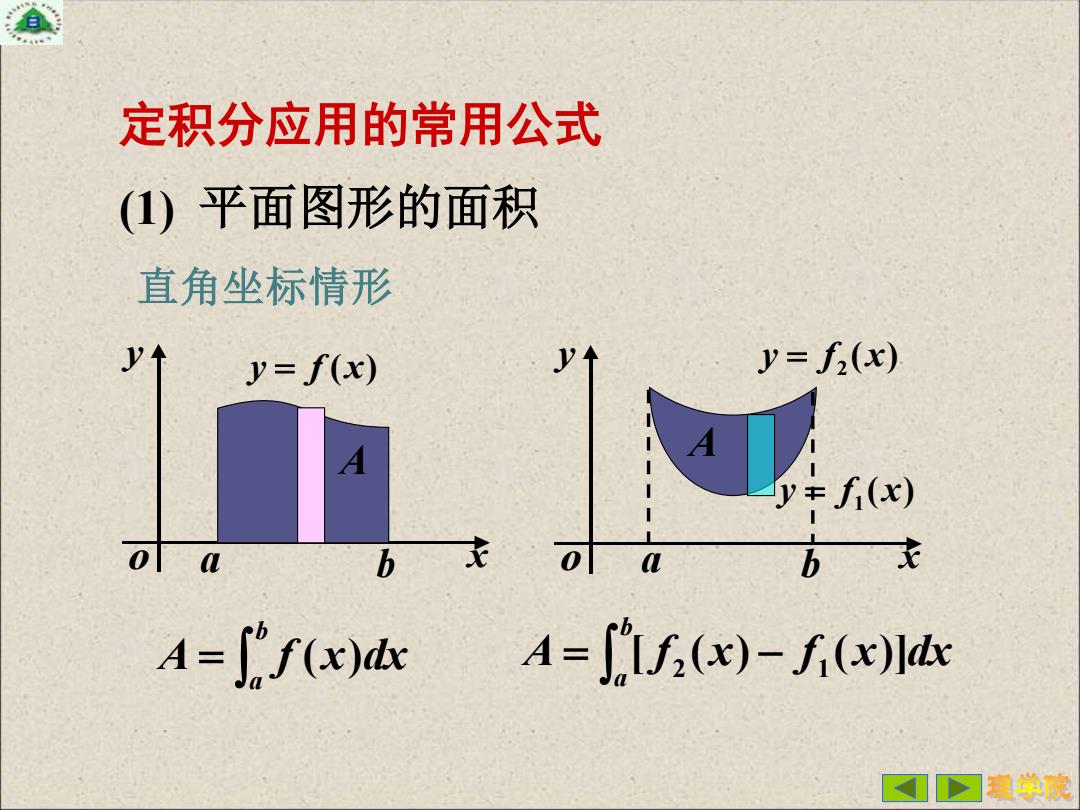
定积分应用的常用公式 (1)平面图形的面积 直角坐标情形 y=f(x) y=f(x) A 年队 A o a b 0 L b末 A=∫fx)c A=l(x)-f(x)ldx >可程学院
定积分应用的常用公式 (1) 平面图形的面积 x y o y = f (x) = b a A f (x)dx x y o ( ) y = f 1 x ( ) y = f 2 x = − b a A [ f2 (x) f1 (x)]dx A A 直角坐标情形 a b a b
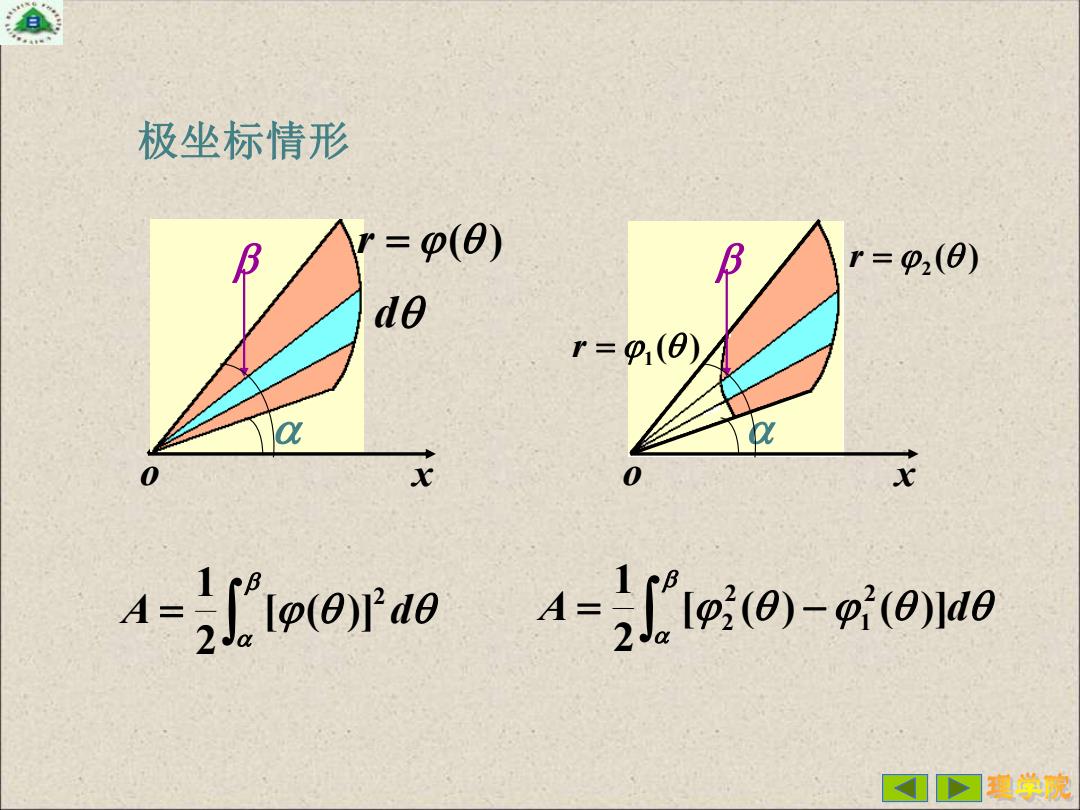
极坐标情形 p(0) r=p2(0) de r=91(0) a 0 X 0 A-iLl(F0 A=i网e-oue ID可程学院
= A d 2 [ ( )] 2 1 o x d r = ( ) o x ( ) r = 2 ( ) r = 1 = − A [ ( ) ( )]d 2 1 2 1 2 2 极坐标情形
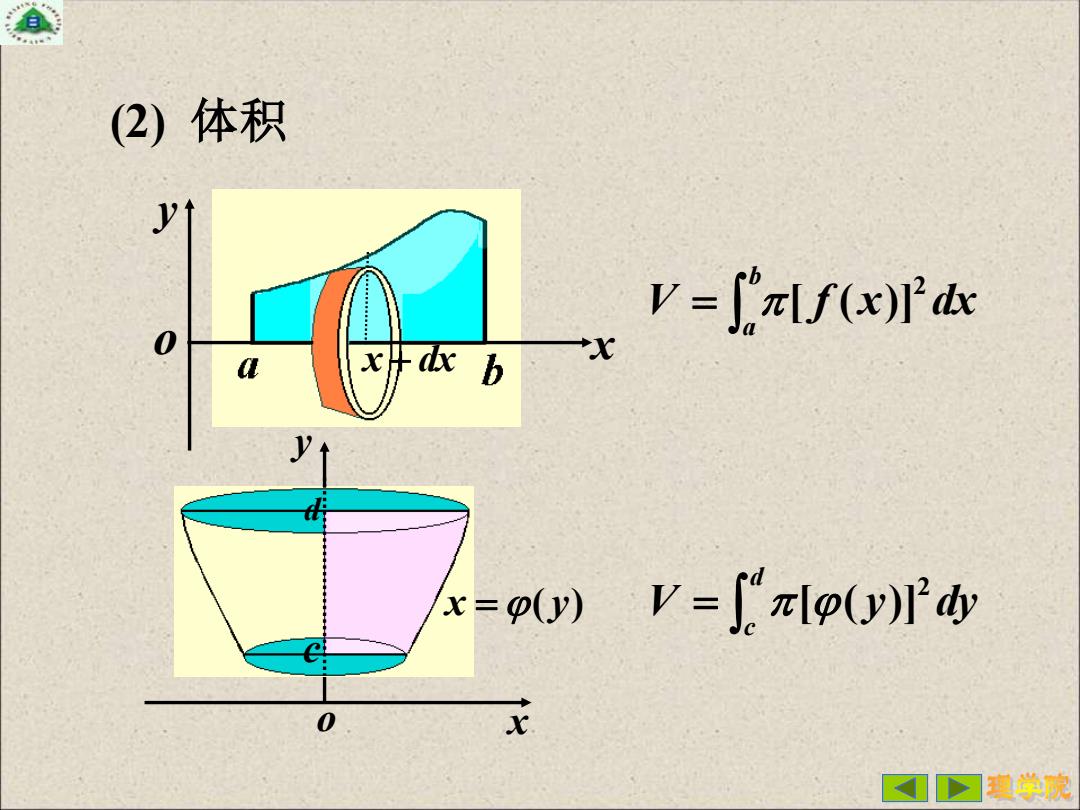
(2)体积 y V=∫fx)dx 0 开b y =o()V=[zlp(y)'dy e 0 >习程学院
(2) 体积 x x + dx x yo V f x dx ba 2 [ ( )] = V y dy dc 2 [( )] = x yo x = ( y) cd
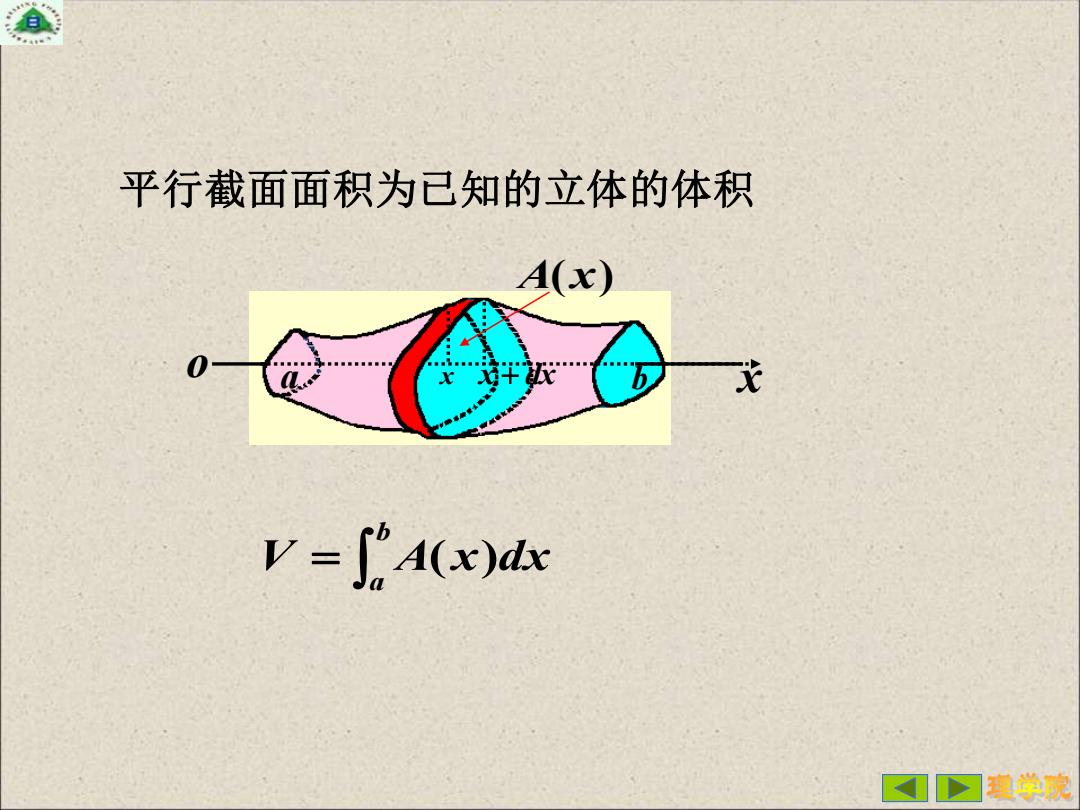
平行截面面积为己知的立体的体积 4(x) 并歌 V=A(x)dx 个>程学院
x o = b a V A(x)dx a x x + dx b 平行截面面积为已知的立体的体积 A(x)
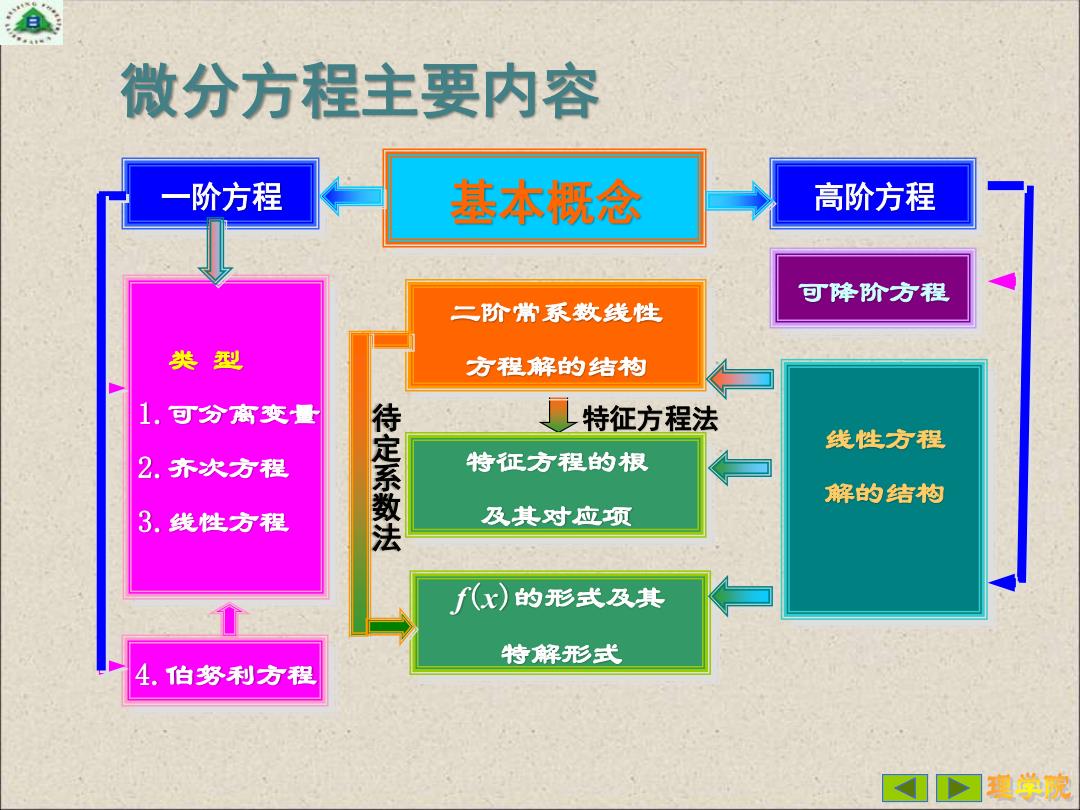
微分方程主要内容 一阶方程 基本概念 高阶方程 可降阶方程 二阶常系数线性 类型 方程解的结构 1.可分高变量 特征方程法 待定系数法 线性方程 2.齐次方程 特征方程的根 解的结构 3.线性方程 及其对应项 f(x)的形式及其 特解形式 4.伯努利方程 ①D可程学院
一阶方程 基本概念 类 型 1.可分离变量 2.齐次方程 3.线性方程 4.伯努利方程 可降阶方程 线性方程 解的结构 二阶常系数线性 方程解的结构 特征方程的根 及其对应项 f(x)的形式及其 特解形式 高阶方程 待 定 系 数 法 特征方程法 微分方程主要内容