点连续 函数y=f(x)在x。处连续1imf(x)=f(x) →X0 特殊:左连续 Iimf(x)=f(xo)右连续1imf(x)=f(x) 概念 x→x0 区间连续 在区间上每一点都连续的函数 函数连续 初等函数 基本初等函数在定义域内是连续的 连续性 切初等函数在其定义区间内都是连续的 M 闭区间上 最大值和最 连续函数 小值定理 性质 有界性定理 y=f( 零点定理 介值定理 52 ✉习程学院
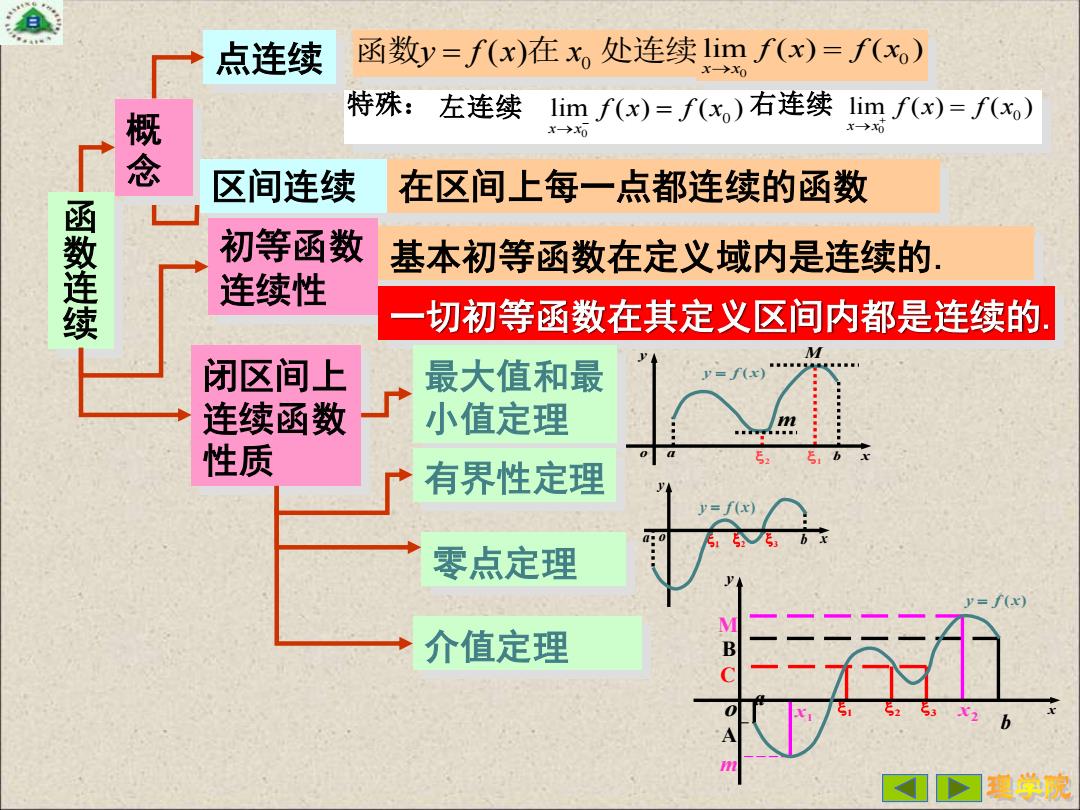
函 数 连 续 概 念 点连续 0 函数y f x x = ( )在 处连续 0 0 lim ( ) ( ) x x f x f x → = 特殊: 左连续 右连续 0 0 lim ( ) ( ) x x f x f x → − = 0 0 lim ( ) ( ) x x f x f x → + = 区间连续 在区间上每一点都连续的函数 初等函数 连续性 基本初等函数在定义域内是连续的. 一切初等函数在其定义区间内都是连续的. 闭区间上 连续函数 性质 最大值和最 小值定理 有界性定理 零点定理 介值定理 M m a b 2 1 x y o y = f (x) a 1 2 3 b x y o y = f (x) M B C A m a b 1 2 3 x1 x2 x y o y = f (x)
导数的定义」 y'=lim y =lim f(x+△x)-f(x) Ax->0 △x △x→0 △x y=f(x) f'(x。)表示曲线y=f(x) 几何意义 在点M(x,f(x)处的 导数的概念 切线的斜率,即 f'(x)=tana, (a为倾角) |y=x-1 函数可导一定连续, 可导与连续 但连续不一定可导: 的关系 高阶导数的定义 (f(x)y'=lim I(x+A)-f(x) △x→0 △x 可D习程学院
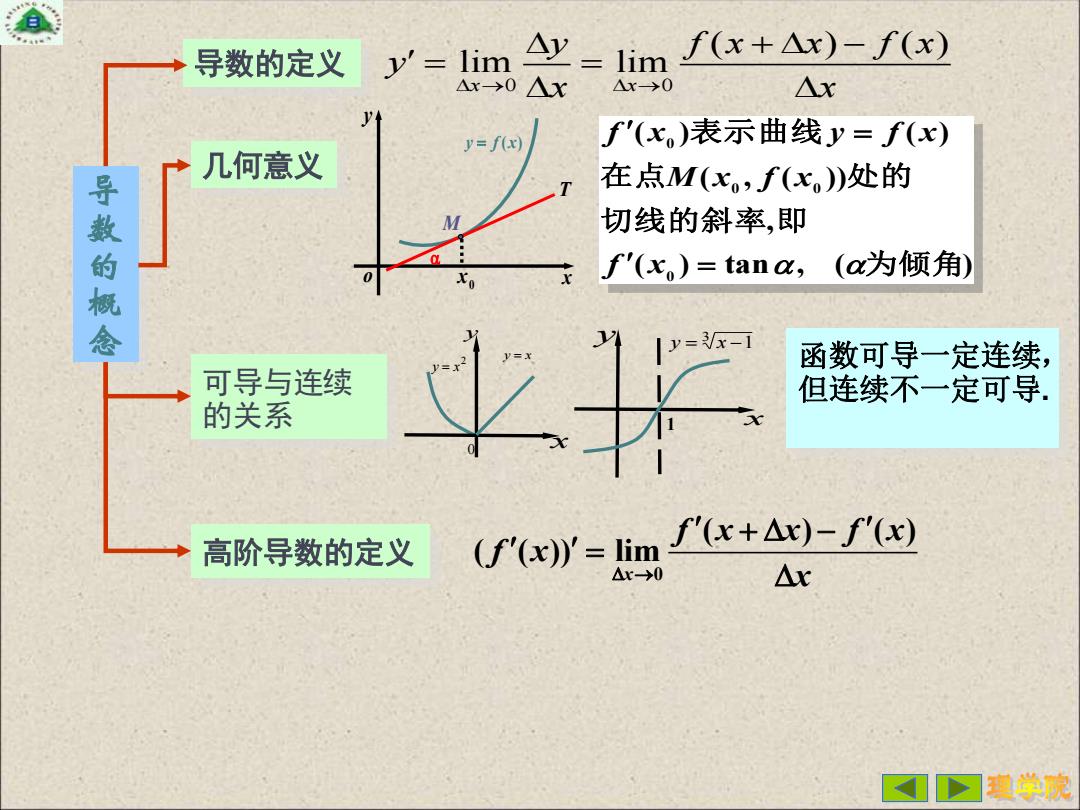
导数的概念 导数的定义 0 0 ( ) ( ) lim lim x x y f x x f x y → → x x + − = = 几何意义 o x y y = f (x ) T 0 x M ( ) tan , ( ) , ( , ( )) ( ) ( ) 0 0 0 0 为倾角 切线的斜率 即 在点 处的 表示曲线 = = f xM x f x f x y f x 可导与连续 的关系 函数可导一定连续, 但连续不一定可导 . x y2 y = x 0 y = x 3 y = x − 1 x y 1 高阶导数的定义 0 ( ) ( ) ( ( )) limx f x x f x f x → x + − =
(I)[u(x)±v(x)'='(x)±v'(x)月 和、差、积、 2)[u(x)·v(x)'=u'(x)v(x)+u(x)v'(x); 商的求导法则 (v(x)≠0) 求导法则 -r国 v2(x) 反函数的导数 导数的运算 复合函数的求导法则 x=,=f'()p'(xo) 基本初等函数 初等函数 或常数的导数 的求导 隐函数求导 直接对方程两边求导, 特殊求导 对数求导法 多个函数相乘和幂指藏()(x)的情形 方法 方法: 先在方程两边取对数然后利用 参数方程所确定的 隐函数的求导方法求出导数 函数的导数 参数方程 x=确定与x间的函数 y=Ψ(t) 方法: 可>可程学院
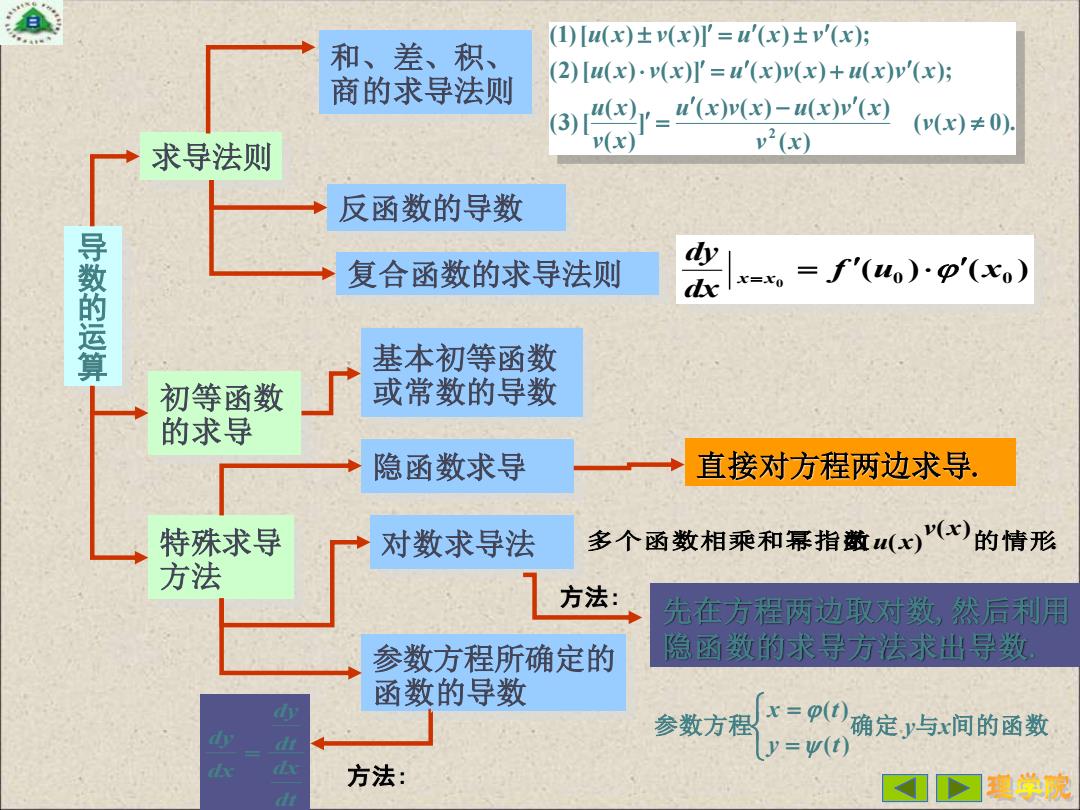
导 数 的 运 算 求导法则 和、差、积、 商的求导法则 ( ( ) 0). ( ) ( ) ( ) ( ) ( ) ] ( ) ( ) (3)[ (2)[ ( ) ( )] ( ) ( ) ( ) ( ); (1)[ ( ) ( )] ( ) ( ); 2 − = = + = v x v x u x v x u x v x v x u x u x v x u x v x u x v x u x v x u x v x 反函数的导数 复合函数的求导法则 ( ) ( ) 0 u0 x0 f dx dy x x = = 初等函数 的求导 基本初等函数 或常数的导数 特殊求导 方法 隐函数求导 直接对方程两边求导. 对数求导法 . ( ) 多个函数相乘和幂指函数 ( ) 的情形 v x u x 方法: 先在方程两边取对数,然后利用 参数方程所确定的 隐函数的求导方法求出导数. 函数的导数 参数方程 确定 y与x间的函数 y t x t = = ( ) ( ) dt dx dt dy dx dy = 方法:
函数y=f(x)在点x,可微y=f(x,+△x)-f()=A△x+o(△x) 微分 可微的条件 可导台可微 A=f'(x0) 微分的求法 求法:计算函数的导数,乘以自变量的微分, 少=f'(x) 微分的几何意义 微分形式的不变性 无论x是自变量还是中间变量函数=f(x)的 微分形式总是='(x) >可程学院
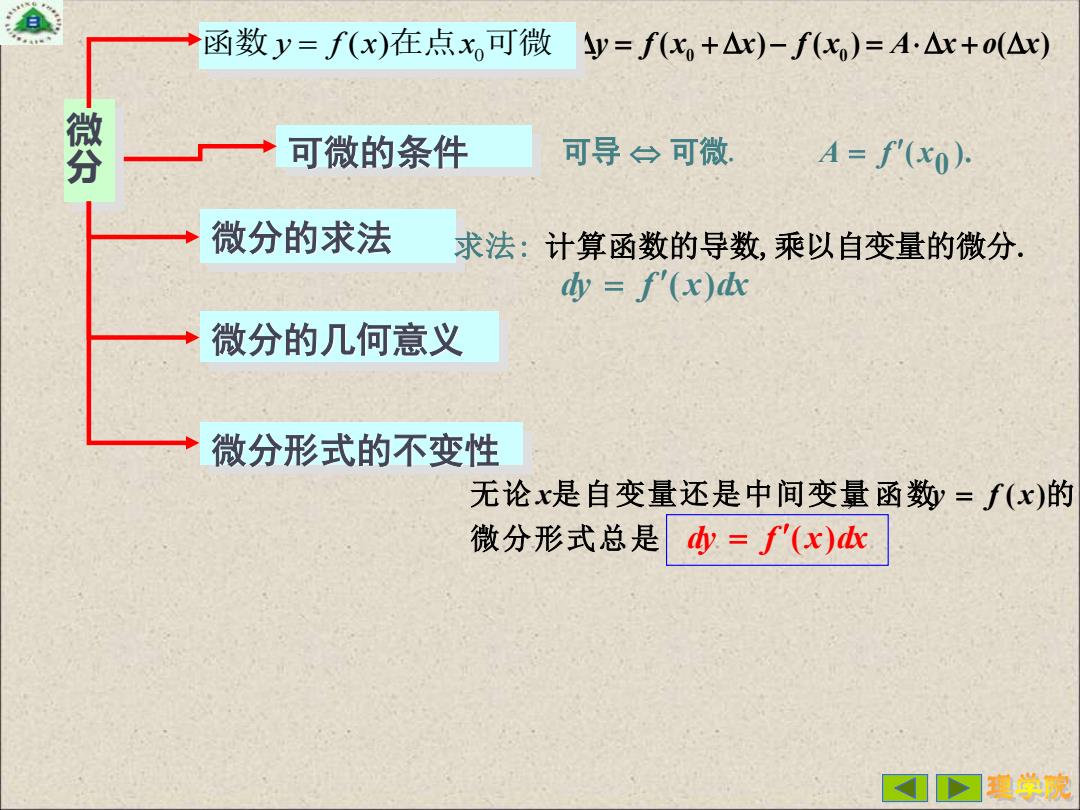
微 分 0 0 = + − = + y f x x f x A x o x ( ) ( ) ( ) 0 函数 y f x x = ( )在点 可微 可微的条件 ). 0 可导 可微. A = f ( x 微分的求法 求法: 计算函数的导数,乘以自变量的微分. dy = f ( x)dx 微分的几何意义 微分形式的不变性 微分形式总是 无 论 x是自变量还是中间变量, 函 数y = f ( x)的 dy = f ( x)dx
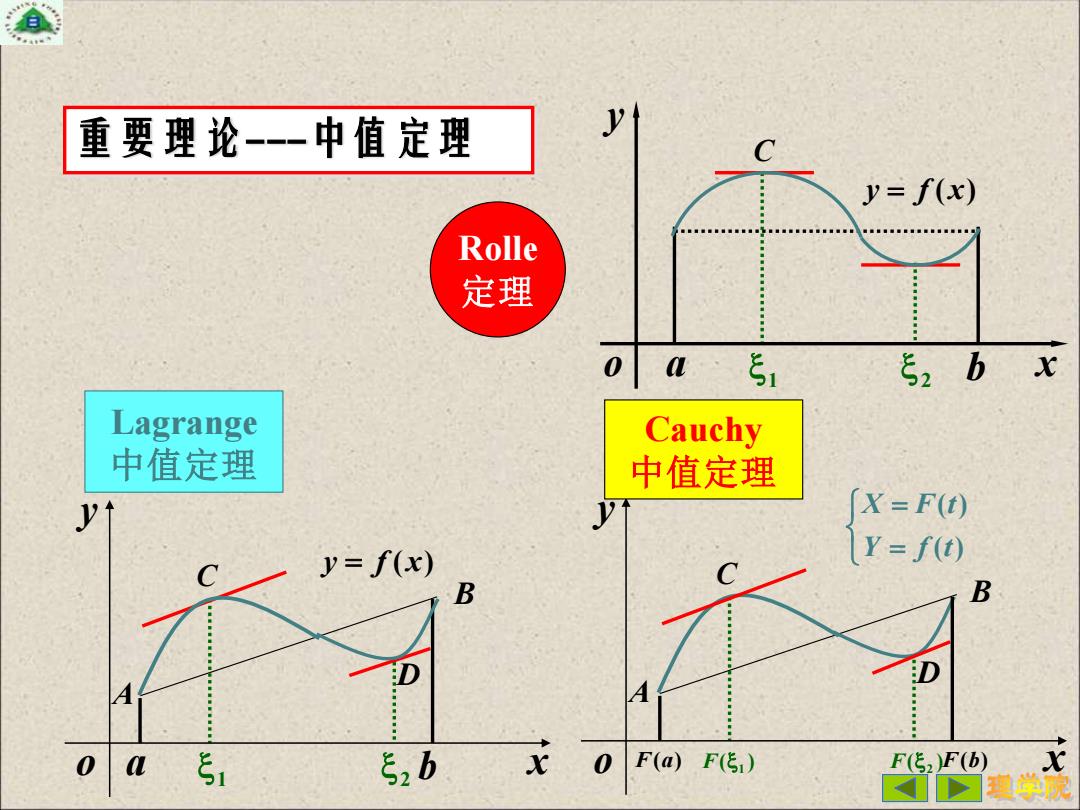
重要理论-一一中值定理 y=f(x) Rolle 定理 0 E2 b x Lagrange Cauchy 中值定理 中值定理 y↑ X=F(t) y=f(x) Y=f(t) C B B o a 5 52b x o F(a)F() F(52)F(b
a 1 2 b x y o y = f (x) C o a 1 2 b x y y = f (x) A B C D ( ) 1 F ( ) 2 o F x y = = ( ) ( ) Y f t X F t F(a) A F(b) B C D Rolle 定理 Lagrange 中值定理 Cauchy 中值定理 重要理论---中值定理