
01函数连续的定义COAOR人邮教育定义1.21如果函数f(x)在开区间(a,b)内每一点都连续,则称f(x)在(a,b)内连续;如果函数f(x)在开区间(a,b)内每一点都连续,且在左端点x=α处右连续,在右端点x=b处左连续,则称f(x)在闭区间a,b上连续,并称a,bu是f(x)的连续区间,注(1)f(x)在左端点x=a处右连续是指满足limf(αx)=f(a)(2)f(x)在右端点x=b处左连续是指满足lim(x)=f(b).X(R)
注 11 如果函数 在开区间 内每一点都连续,则 称 在 内连续;如果函数 在开区间 内每 一点都连续,且在左端点 处右连续,在右端点 处 左连续,则称 在闭区间 上连续,并称 是 的连续区间. (1) 在左端点 处右连续是指满足 . (2) 在右端点 处左连续是指满足 . 定义1.21 01 函数连续的定义
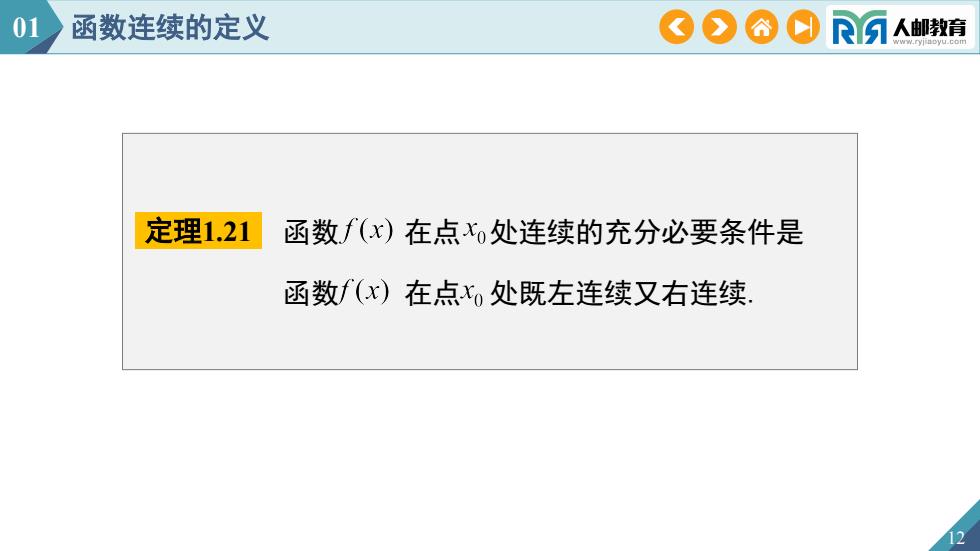
01函数连续的定义COAR人邮教育定理1.21函数f(x)在点xo处连续的充分必要条件是函数f(x)在点xo处既左连续又右连续
定理1.21 12 函数 在点 处连续的充分必要条件是 函数 在点 处既左连续又右连续. 01 函数连续的定义

O060人邮教育RA0<x<1,ix,例11设f(x)=x = 1211,1<x<2.(1)求x?1时,f(x)的左极限和右极限。(2)f(x)在x=1处连续吗?(3)求f(x)的连续区间[
13 (1)求 时, 例 1 设 的左极限和右极限。 (2) 在 处连续吗? (3)

R人邮教育本讲内容w.nvlnDyu.c01函数连续的定义02函数的间断点03连续函数的性质04闭区间上连续函数的性质
01 函数连续的定义 02 函数的间断点 03 连续函数的性质 04 闭区间上连续函数的性质 本 讲 内 容

02OOOOR函数的间断点人邮教育定义1.22如果函数f(x)在点xo处不连续,则称函数f(x)在点xo处间断,点xo称为f(x)的间断点.显然,如果在点xo处有下列3种情形之一,则点x称为f(α)的间断点:(1在点Xo处没有定义:在点xo处极限lim()不存在;虽然f(x)有定义,limf(x)存在,但limf(x)’f(xo)XRX
15 (1 ) 在点 处没有定义; 定义1.22 如果函数 在点 处不连续, 则称函数 在点 处间断,点 称为 的间断点.显然, (2 ) 在点 处极限 不存在; (3 ) 虽然 有定义, 存在, 但 处有下列3种情形之一,则点 称为 的间断点: 02 函数的间断点 如果在点