
动量守恒定律 质点所受合外力为零时,质点的动量保持不变 条件:∑F=0 若F=0则 D=mv=c 意义:质点不受外力作用时,动量保持不变 分量形式:若F≠0但F=0则卫x=m心=C 动量守恒定律是物理学中最重要、最普遍的定律之一, 它不仅适合宏观物体,同样也适合微观领域。 电身排拉
质点所受合外力为零时, 质点的动量保持不变 条件: 动量守恒定律 动量守恒定律是物理学中最重要、最普遍的定律之一, 它不仅适合宏观物体,同样也适合微观领域。 F 0 p mv c F 0 0 Fx p mx c 分量形式:若 但 则 x 意义:质点不受外力作用时,动量保持不变. 若 则
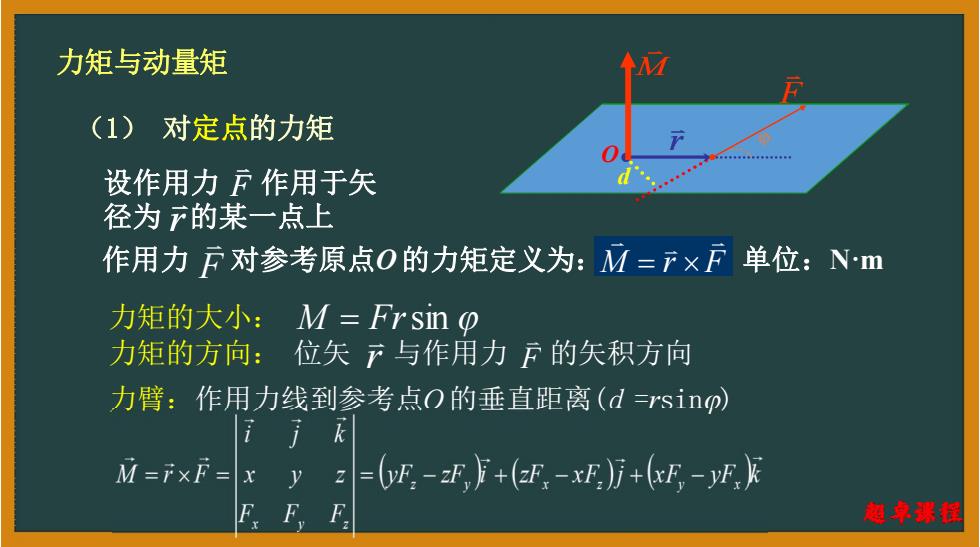
力矩与动量矩 (1)对定点的力矩 设作用力户作用于矢 径为下的某一点上 作用力F对参考原点O的力矩定义为:M=FxF单位:Nm 力矩的大小:M=Frsin O 力矩的方向:位矢下与作用力的矢积方向 力臂:作用力线到参考点O的垂直距离(d=rsing) i i M=FxF- (-zE,+(E-x)万+(E,-F 电卓球拉
(1) 对定点的力矩 设作用力 作用于矢 径为 的某一点上 F r M r F M r F 作用力 F 对参考原点O 的力矩定义为: 单位:N·m F r O d M 力矩与动量矩 力矩的大小: M Frsin 力矩的方向: 位矢 与作用力 F 的矢积方向 r 力臂:作用力线到参考点O 的垂直距离(d =rsin)
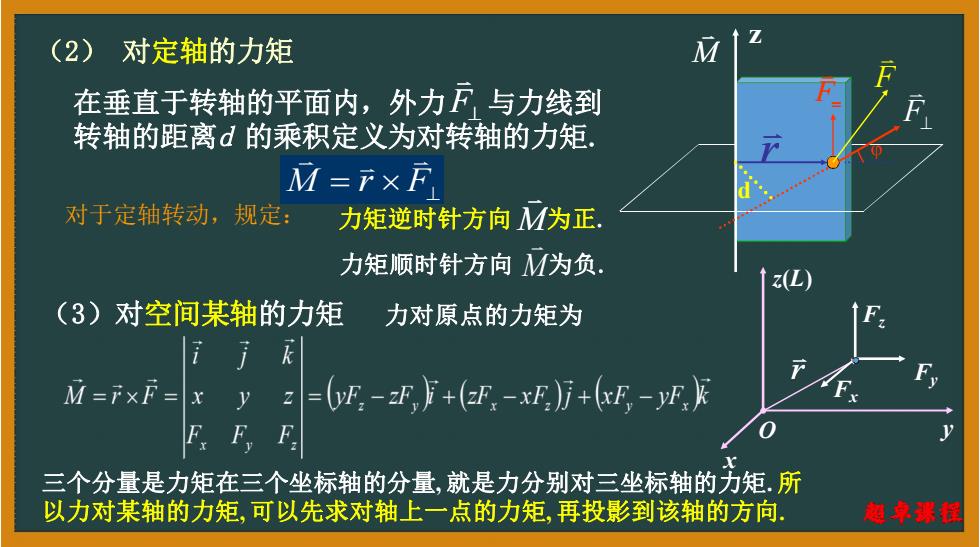
(2) 对定轴的力矩 在垂直于转轴的平面内,外力F与力线到 转轴的距离d的乘积定义为对转轴的力矩. M=F×F 对于定轴转动,规定: 力矩逆时针方向M为正 力矩顺时针方向M为负. (3)对空间某轴的力矩 力对原点的力矩为 i j M=FxF=x =(p-z,+(-xE)月+-y)足 FFF 三个分量是力矩在三个坐标轴的分量,就是力分别对三坐标轴的力矩.所 以力对某轴的力矩,可以先求对轴上一点的力矩,再投影到该轴的方向. 泡早排拉
z F r F d 在垂直于转轴的平面内,外力 与力线到 转轴的距离d 的乘积定义为对转轴的力矩. F F M r 对于定轴转动,规定: 力矩逆时针方向 M为正. 力矩顺时针方向 M为负. M F (2) 对定轴的力矩 (3)对空间某轴的力矩 力对原点的力矩为 r Fx y z(L) Fy Fz O x 三个分量是力矩在三个坐标轴的分量, 就是力分别对三坐标轴的力矩. 所 以力对某轴的力矩, 可以先求对轴上一点的力矩, 再投影到该轴的方向