《线性代数》课程教学资源（PPT课件）第三章 矩阵的初等变换及线性方程组 3.3 线性方程组的解

x1+x2-2x3+x4=4(I) (3)>(4) (B3 0> X2-x3+x4=0(2) (B4) (4)-2(3) x4=-3(3) 0=0(4) 一Ax=b (2)-(3) (1)(2) (3)-2(1) (3)-(4) (B)> (B)→(B2)→ (B3)>(B4), (3)÷2 (4)-31) (3)+5(2 (4)-2(3) (4)-3(2) 同解 Ax=b Ax=b

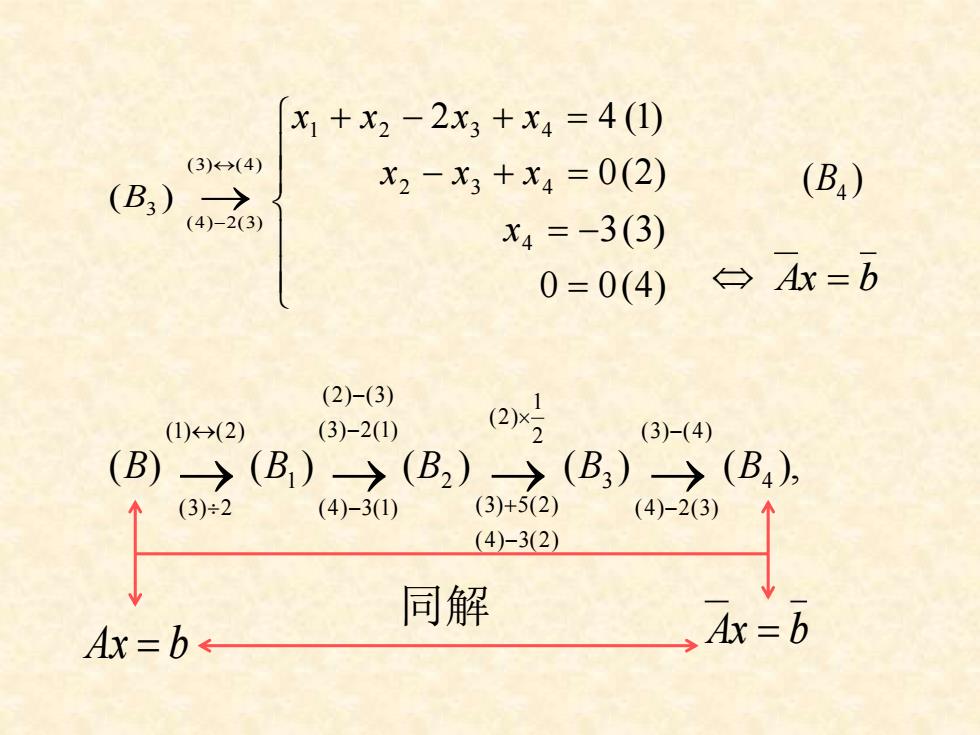
( ) B3 →  − (3) (4) (4) 2(3)         = = − − + = + − + = (4) (3) (2) ( ) 0 0 3 0 2 4 4 2 3 4 1 2 3 4 x x x x x x x x ( ) B4 ( ) ( ) ( ) ( ) ( ), 4 (3) (4) (4) 2(3) 3 2 1 (2) (4) 3(2) (3) 5(2) 2 (3) 2(1) (2) (3) (4) 3(1) 1 (1) (2) (3) 2 B → B → B → B → B − −  − + − − −   同解  Ax = b Ax = b Ax = b

2-1-1 12 11-214 1 1 -2 1 4 01-1 1 0 B=(A,b)= =(A,b) 4 -62 -24 00 01 3 6-97 9 00000 (2)-(3) (1)→(2) (3)-2() a (3)-(4) →(B)>(B2)→(B)→(B4)=(A,b), (3)÷2 (4)-3(1) (3)+52) (4)-2(3) (4)-3(2) 求解Ax=b台求解Ax=b

              − − − − − − = 3 6 9 7 9 4 6 2 2 4 1 1 2 1 4 2 1 1 1 2 ( ) ( ) ( ) ( ) ( , ), 4 (3) (4) (4) 2(3) 3 2 1 (2) (4) 3(2) (3) 5(2) 2 (3) 2(1) (2) (3) (4) 3(1) 1 (1) (2) (3) 2 → B → B → B → B = A b − −  − + − − −   ～ r B= (A,b) 求解Ax = b  求解Ax = b r ( , ) 0 0 0 0 0 0 0 0 1 3 0 1 1 1 0 1 1 2 1 4 = A b               − − −

矩阵初等行变换可以求解线性方程组， 定理：线性方程组经初等变换，解 不变

矩阵初等行变换可以求解线性方程组. 定理：线性方程组经初等变换，解 不变

二、线性方程组的解法 用初等变换求解Ax=b: ①B=(A,b)”→(A,b):行最简形，求R(A),R(B) ②判别（定理1）： R(A)KR(B),则Ax=b无解。 R(4)=R(B,则有解F有唯一解。 <n,有无穷多个解。 ③ x=的解即是Ax=b的解

二、线性方程组的解法 用初等变换求解Ax = b： B (A,b) (A,b) : R(A), R(B). = ⎯r → 行最简形，求 R(A)R(B),则Ax = b无解。   = = 有无穷多个解。 有唯一解。 则有解 , , ( ) ( ), n n R A R B  Ax = b的解即是Ax = b的解。 ① ② ③ 判别（定理1）：