
几何意义 它是介于x轴、函数f(x)的图形及两条 直线x=a,x=b之间的各部分面积的代数和。 在x轴上方的面积取正号;在x轴下方的面 积取负号 ff(x)dx=-A+A-A 2012329 泰山医学院信息工程学院高等数学教研室

例1利用定义计算定积分xd. 解(①)分割 将0,n等分,分点为x,=, (i=1,2,m) 小区间k1的长度Ax”G=12,心 (2)取点取5=x,(i=1,2,n) (3)求和2f5)Ax=25ax,=立Ax, 2012329 奉山医学院信息工程学院高等数学教研常

=21=-1.a+1x2m+n 台n)nn3台 n3 6 n 元→0→n→w (4)求极限x=im2Ax, 2→01 1 lim n→o6 2012329 奉山医学院信息工程学院高等数学教研常
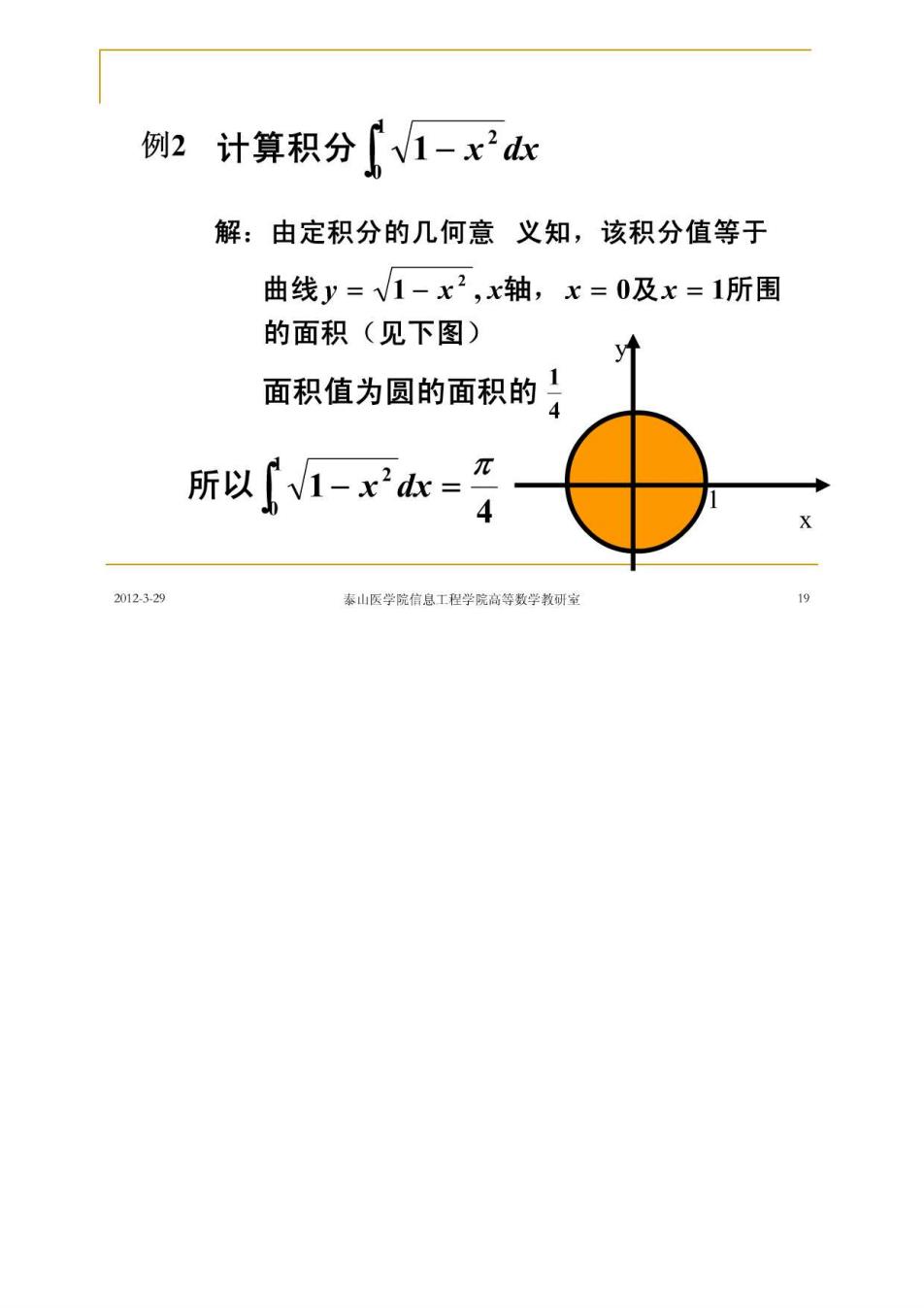
例2计算积分1-x2dk 解:由定积分的几何意义知,该积分值等于 曲线y=√1-x2,x轴,x=0及x=1所围 的面积(见下图) 面积值为圆的面积的! π 所以V1-x2d= 2012329 奉山医学院信息工程学院高等数学教研常

五定积分的性质 对定积分的补充规定: (1)当a=b时,f(x)dk=0: 2)[f(x)dx=-[f(x)dx. 注意在下面的性质中,假定定积分都存 在,且不考虑积分上下限的大小. 2012329 素山医学院信息工程学院高等数学教研室