
注: ()利用极限的“£-6”的说法,将定积分的 定义精确表述如下: [f(x)dx=I=lim>f()Ax →01 H8>0,36>0,对于区间[a,b1的任何分法,不论5, 在x,-1,x,中怎样取法,只要2<6,有 空A-1C 成立,则称I是f(x)在区间a,b上的定积分. 2012329 素山医学院信息工程学院高等数学教研举 11

(2)积分值仅与被积函数及积分区间有关, 而与积分变量的写法无关, [f(x)dx [f(N)dt=[f(u)du (3)积分值与区间的分法和5:的取法是无关的 (4)当函数f(x)在区间a,b]上的定积分存在时, 称f(x)在区间[a,b]上可积. 2012329 奉山医学院信息工程学院高等数学教研常

(5)曲边梯形由连续曲线y=f(x)(f(x)≥0)、 x轴与两条直线x=a、x=b所围成。 其面积A等于函数f(x)在区间[a,b上的定积分, 即 A=[f(x)dx (⑥)设某质点作直线运动,速度v=v(t)是时 间间隔T,T,]上1的一个连续函数,物体在这 段时间内所经过的路程 S=[v(t)dt 2012329 素山医学院信息工程学院高等数学教研常

三 定积分存在的两个充分条件 定理1设函数f(x)在区间a,b1上连续, 则f(x)在区间a,b]上可积, 定理2设函数f(x)在区间a,b]上有界, 且只有有限个间断点,则f(x)在 区间a,b1上可积. 注意这两个定理仅仅是充分条件,不是必要的。 2012329 素山医学院信息工程学院高等数学教研室 14
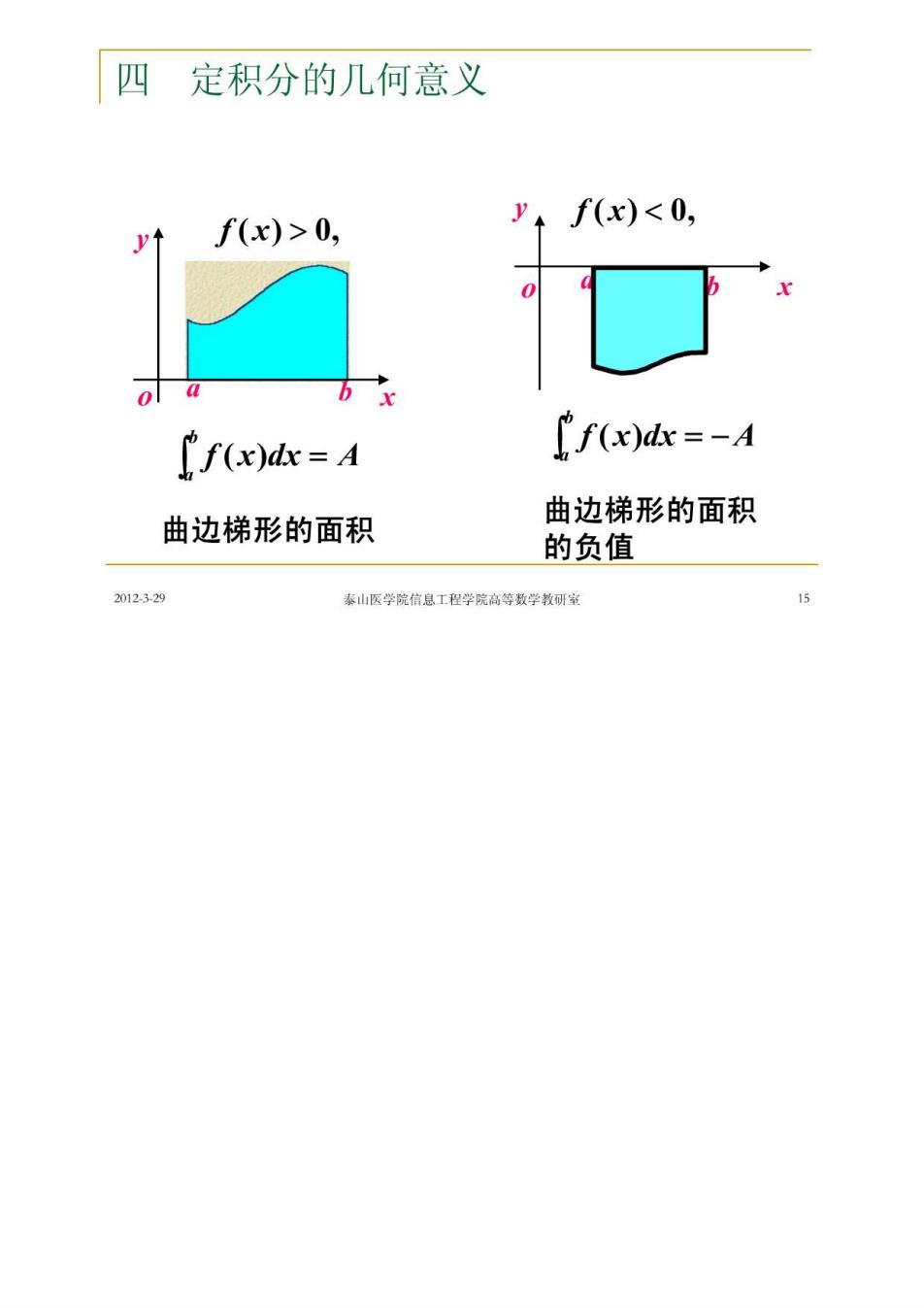
四定积分的几何意义 f(x)>0, y+f(x)<0, o a [f(x)d=A [f(x)dx=-A 曲边梯形的面积 曲边梯形的面积 的负值 2012329 素山医学院信息工程学院高等数学教研常