《线性代数》课程教学课件（讲稿，B）§4.3 非齐次线性方程组

x=k151+k252+.+kn-,5m-,+7 而由性质4.32可知，对任何数k1,k2,km- 上式总是方程(4-1)的解， 1.于是方程组(4-1)的通解为 x=k51+k52+.+km-,5m-,+7 其中51,52，5n-,是(4-5)式的基础解系， k1,k2,kn,为任意数，n是(4-1)的特解

上式总是方程(4-1)的解, * 1 1 2 2 n r n r x k k k           而由性质4.3.2可知,对任何数 1 2 , , , n r k k k   1 2 , , , n r    其中   是(4-5)式的基础解系, * 1 1 2 2 n r n r x k k k           1.于是方程组(4-1)的通解为 1 2 , , , n r k k k   为任意数, (4 1) .  * 是  的特解

2.例题1.求解方程组 X1+X2-3x3-x4=1, 3x1-x2-3x3+4x4=4, x1+5x2-9x3-8x4=0. 解：对增广矩阵进行初等行变换化成行最简形 [11-3-1113-3r「11-3 -11 A- 3- 1-3 44 0-4 6 71 15-9 -803-104-6 -7-1

1 2 3 4 1 2 3 4 1 2 3 4 3 1, 3 3 4 4, 5 9 8 0. x x x x x x x x x x x x                  2.例题1.求解方程组 1 1 3 1 1 3 1 3 4 4 1 5 9 8 0 A                  2 1 3 1 3 1 1 3 1 1 ~ 0 4 6 7 1 0 4 6 7 1 r r r r                   解： 对增广矩阵进行初等行变换化成行最简形

「11-3 -1 1 3 3 5 5+2 0 1 3 01 7 1 2 4 3 7 1 5x-300000 2 4 4 01 2 -4 00 0 0 0 于是得与原方程组同解的方程组 3 5 x3 2 X4= 4 3 7 1 2 2 4 4

3 2 2 1 1 3 1 1 3 7 1 ~ 0 1 244 1 ( ) 0 0 0 0 0 4 r r r                   1 2 3 3 5 1 0 2 4 4 3 7 1 ~ 0 1 244 0 0 0 0 0 r r                  于是得与原方程组同解的方程组 1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 , 2 4 4 x x x x x x            

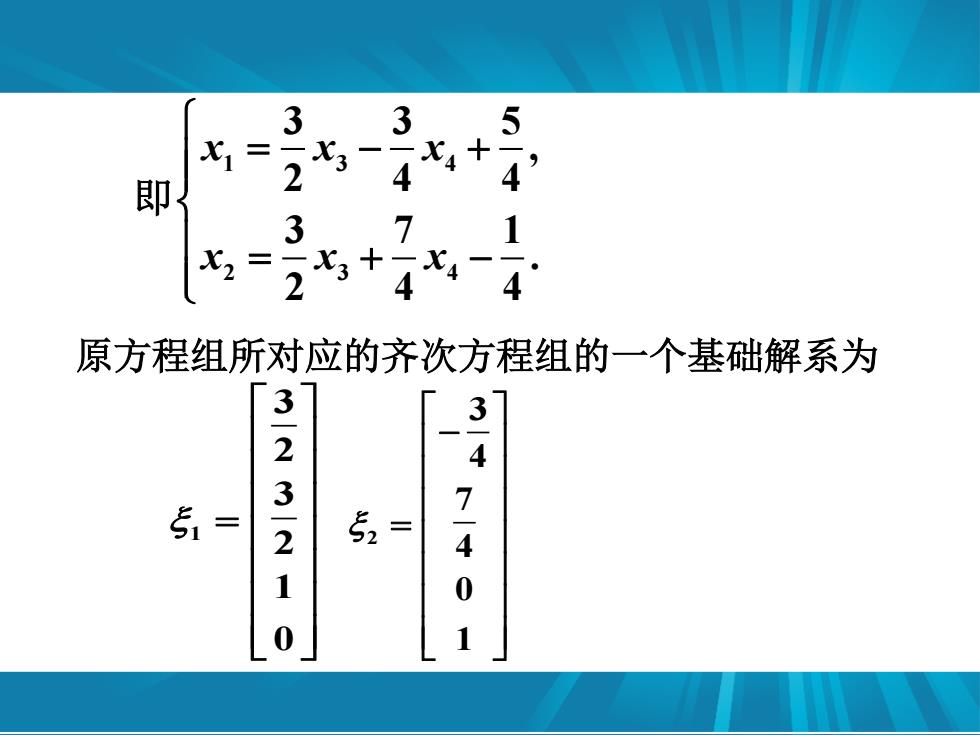
3 3 5 X1= 尤4+ 即 2 4 3 7 1 ×2 2 4 原方程组所对应的齐次方程组的一个基础解系为 3 3 2 4 3 51= 7 52= 1 0 0 1

1 3 4 2 3 4 3 3 5 , 2 4 4 3 7 1 . 2 4 4 x x x x x x            即 原方程组所对应的齐次方程组的一个基础解系为 1 3 2 3 2 1 0                     2 3 4 7 4 0 1                    

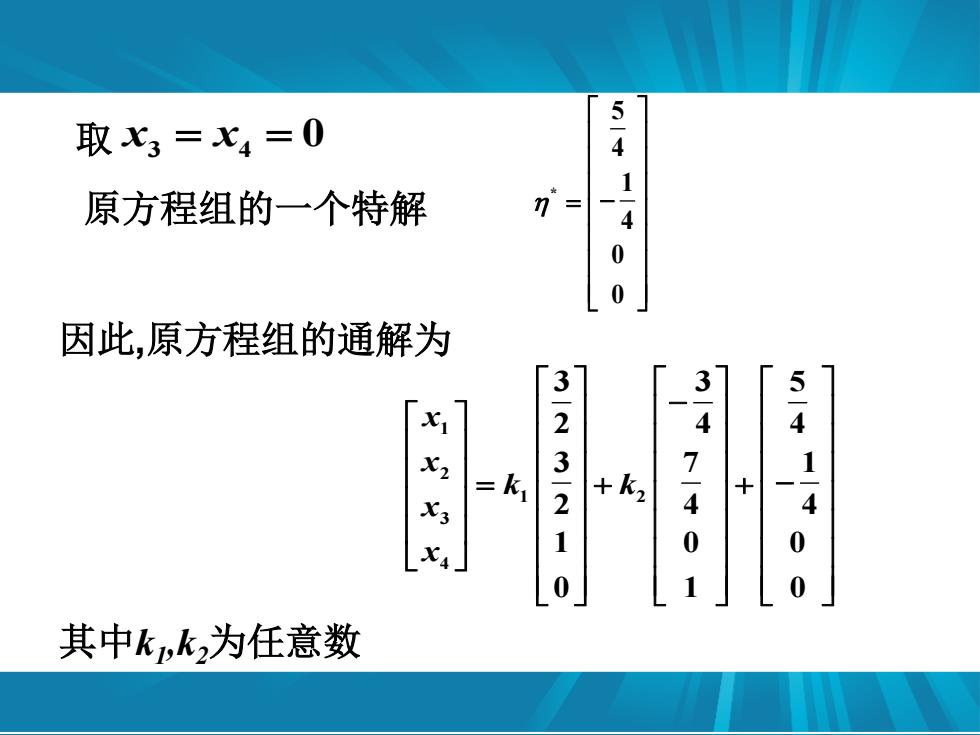
取x3=X4=0 5-4 原方程组的一个特解 7= 14 因此，原方程组的通解为 4 5-4 =k1 3-2 +k2 7-4 + 1 0 140 0】 0 其中k,k,为任意数

取 x x 3 4   0 原方程组的一个特解 * 5 4 1 4 0 0                      1 2 1 2 3 4 3 3 5 2 4 4 3 7 1 2 4 4 1 0 0 0 1 0 x x k k x x                                                                        因此,原方程组的通解为 其中k1 ,k2为任意数