
概率论与散理统计 第三节 协方差及相关系数 一、协方差的概念及性质 二、相关系数的概念及意义
一、协方差的概念及性质 二、相关系数的概念及意义 第三节 协方差及相关系数

概率论与散理统外「 一、协方差的概念及性质 1.问题的提出 D(X+Y)=D(X)+D(Y)+2E[X-E(X)]Y-E(Y) 若随机变量X和Y相互独立,那么 D(X+Y)=D(X)+D(Y)
1. 问题的提出 若随机变量 X 和Y 相互独立,那么 D(X Y ) D(X) D(Y ). D X Y D X D Y E X E X Y E Y ( ) ( ) ( ) 2 {[ ( )][ ( )]}. 一、协方差的概念及性质

概率论与敖理统计 2.协方差(Covariance)的定义 量E{[X-E(X)IY-E(Y)}称为随机变量 X与Y的协方差.记为Cov(X,Y),即 Cov(X,Y)=EX-E(X)]Y-E(Y)] 3.协方差的计算公式 Cov(X,Y)=E(XY)-E(X)E(Y)
Cov( , ) {[ ( )][ ( )]}. . Cov( , ), {[ ( )][ ( )]} X Y E X E X Y E Y X Y X Y E X E X Y E Y 与 的协方差 记为 即 量 称为随机变量 2. 协方差( Covariance )的定义 3. 协方差的计算公式 Cov( X,Y) E(XY) E(X )E(Y)

概率伦与散理统针」 4.性质 Cov(X,Y)=E(XY)-E(X)E(Y) (1)Cov(X,Y)=Cov(Y,X); (2)Cov(X,bY)=bCov(X,Y),a,b为常数; (3)Cov(Xi+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
4. 性质 (1) Cov(X,Y ) Cov(Y, X); (2) Cov(aX,bY ) abCov(X,Y ), a, b 为常数; (3) Cov( , ) Cov( , ) Cov( , ). X1 X2 Y X1 Y X2 Y Cov( X ,Y ) E( X Y ) E( X )E(Y )
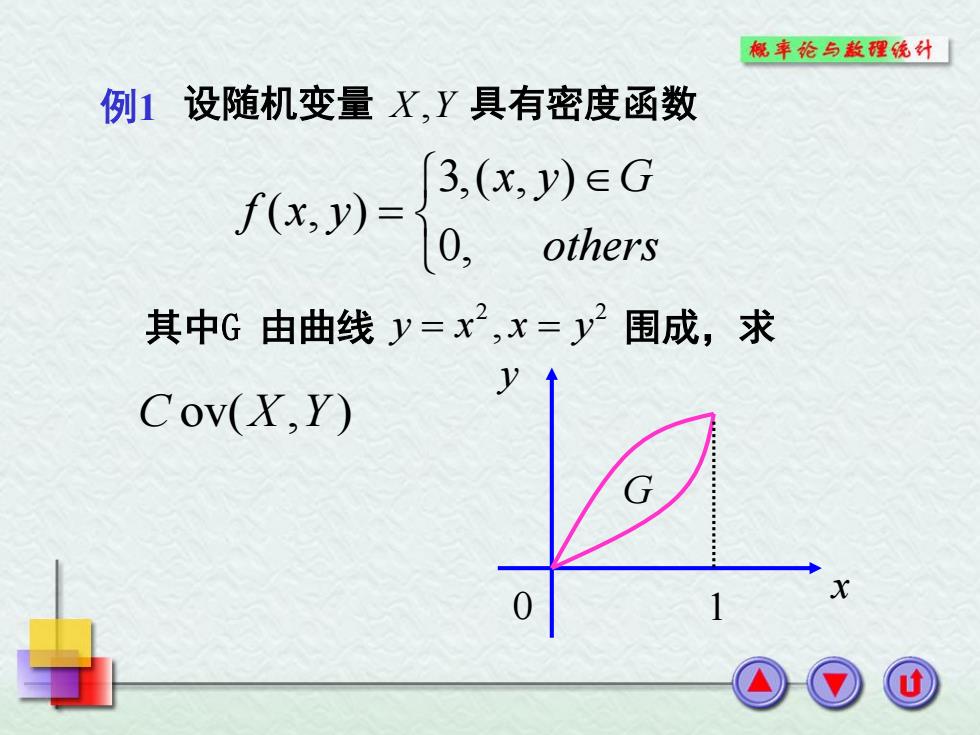
概率论与敖理统外 例1设随机变量X,Y具有密度函数 .)-(EG 0, others 其中G由曲线y=x2,x=y2围成,求 y Cov(X,Y)
例1 设随机变量 X Y, 具有密度函数 3,( , ) ( , ) 0, x y G f x y others 其中G 由曲线 2 2 y x x y , 围成,求 C X Y ov( , ) y x 0 1 G