《概率论与数理统计》课程教学课件（PPT讲稿，48学时）第三章 多维随机变量及其分布 第二节 边缘分布

第二节边缘分布 一、边缘分布函数 二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘概率密度

二、离散型随机变量的边缘分布律 三、连续型随机变量的边缘概率密度 一、边缘分布函数 第二节 边缘分布

问题：已知(X,Y)的分布，如何确定X的分布？ ↓ F(x,y)=P{X≤x,Y≤y},Fx(x)=P{X≤x}, P{X≤x}=P{X≤x,Y<o}=F(x,o)=Fx(x) I (X,Y)关于X的边缘分布函数

问题: ( , ) , ? 已知 X Y X 的分布 如何确定 的分布 F(x, y)  P{X  x,Y  y}, F (x) P{X x}, X   P{X  x}  P{X  x,Y  }  F(x,) F (x)  X (X,Y )关 于X的边缘分布函数

一、边缘分布函数 定义设F(x,y)为随机变量(X,Y)的分布函数， 则F(x,y)=P{X≤x,Y≤y以. 令y→0，称P{X≤x}=P{X≤x,Y<o}=F(x,o) 为随机变量(X,Y)关于X的边缘分布函数 记为Fx(x)=F(x,o): 同理令x→0， Fy(y)=F(o,y)=P{X<∞，Y≤y}=P{Y≤y} 为随机变量(X,Y)关于Y的边缘分布函数

F ( y) F( , y) P{X ,Y y} P{Y y} Y         为随机变量 ( X,Y )关于Y 的边缘分布函数. ( , ) ( , ) , ( , ) { , }. , { } { , } ( , ) ( , ) . F x y X Y F x y P X x Y y y P X x P X x Y F x X Y X             设 为随机变量 的分布函数 则 令 称 为随机变量 关于 的边缘分布函数 F (x)  F(x,). 记为 X 定义 同理令 x  , 一、边缘分布函数

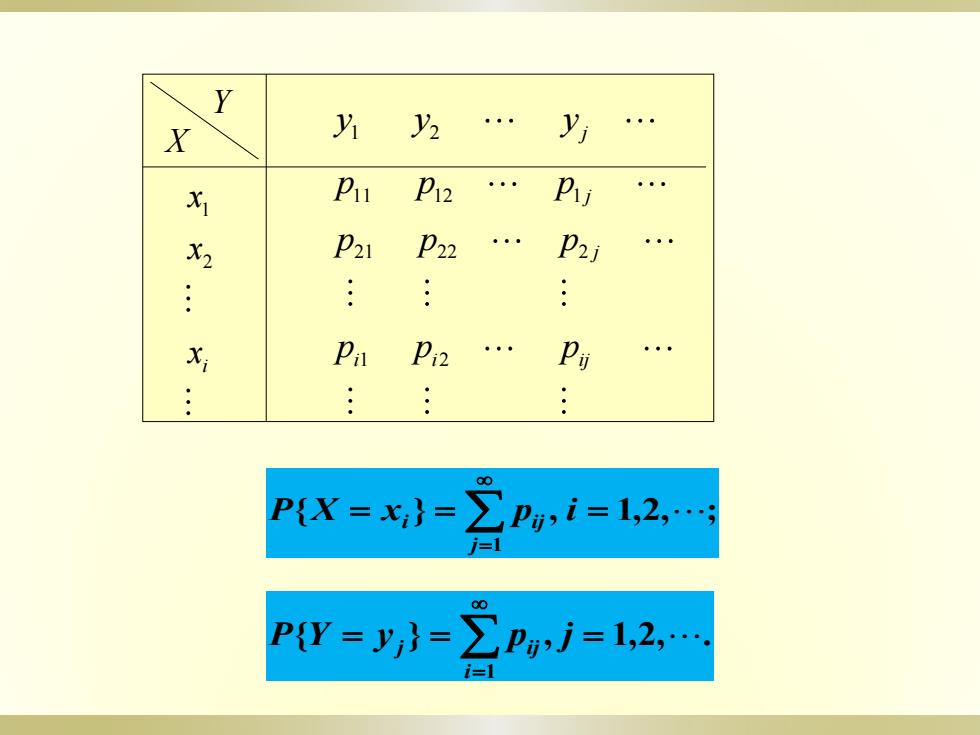
二、离散型随机变量的边缘分布律 定义设二维离散型随机变量(X,Y)的联合分布 律为 P{X=x,Y=yj}=Pi,j=1,2,. 记 p.=∑pg=PX=xhi=1,2y i=1 p=P防=PY=y,j=12,. i1 分别称p.(i=1,2,)和p.(j=1,2,)为(X,Y) 关于X和关于Y的边缘分布律

. ( 1,2, ) ( 1,2, ) ( , ) { }, 1,2, , { }, 1,2, , { , } , , 1,2, . ( , ) 1 1 关于 和关于 的边缘分布律 分别称 和 为 记 律为 设二维离散型随机变量 的联合分布 X Y p i p j X Y p p P Y y j p p P X x i P X x Y y p i j X Y i j j i j ij i j i ij i j ij                              二、离散型随机变量的边缘分布律 定义

X y X P11 p12 P x2 P21 P22 . P2i x Pa Pi2 Pi PX=}=Pg,i=12, i= PY=y}=∑Pj=1,2

{ } , 1,2, ; 1        P X x p i j i ij { } , 1,2, . 1        P Y y p j i j ij X Y 1 2 i x x x 1 2 j y y y 11 12 1 21 22 2 1 2 j j i i ij p p p p p p p p p