
第三节条件分市 一、离散型随机变量的条件分布 二、连续型随机变量的条件分布
一、离散型随机变量的条件分布 二、连续型随机变量的条件分布 第三节 条件分布

一 离散型随机变量的条件分布 定义设(X,)是二维离散型随机变量,对于固定 的j,若P{Y=y}>0,则称 P(X=xY=Yj}= P{X=x,Y=y》}P P(Y=y} p 为在Y=y条件下随机变量X的条件分布律
. , { } { , } { } , { } 0, ( , ) , 为在 条件下随机变量 的条件分布律 的 若 则称 设 是二维离散型随机变量 对于固定 Y y X p p P Y y P X x Y y P X x Y y j P Y y X Y j j ij j i j i j j 定义 一、离散型随机变量的条件分布

对于固定的i,若P{X=x}>0,则称 PW=yX=}=PX==吃, P(X=x} 为在X=x,条件下随机变量Y的条件分布律。 其中i,j=1,2
. , { } { , } { } , { } 0, 为在 条件下随机变量 的条件分布律 对于固定的 若 则称 X x Y p p P X x P X x Y y P Y y X x i P X x i i ij i i j j i i 其中i, j 1,2,
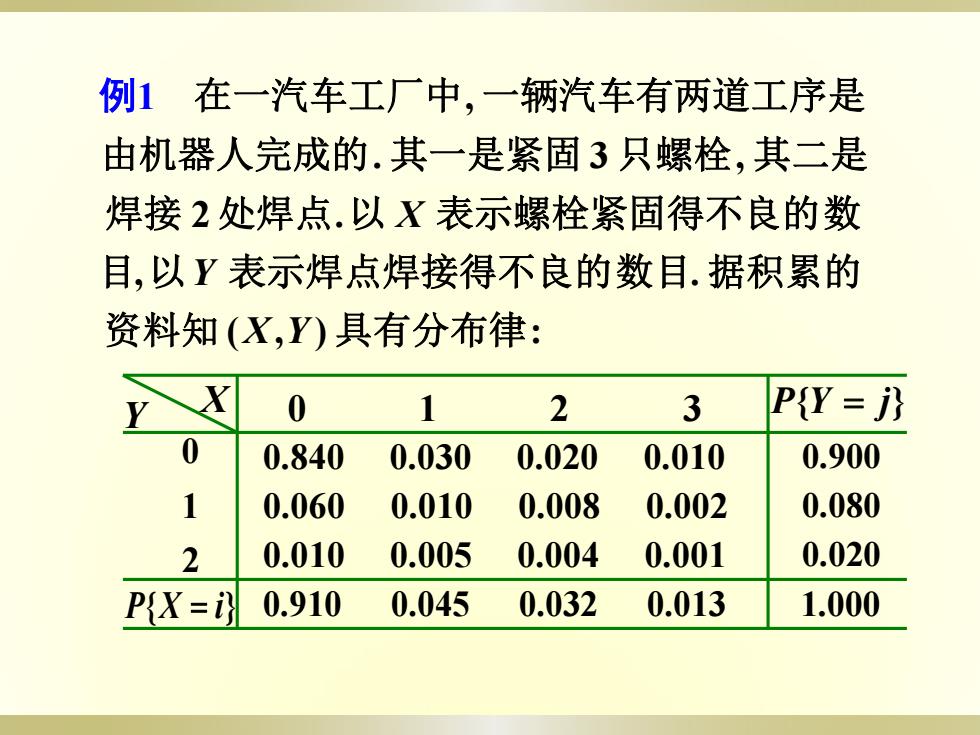
例1在一汽车工厂中,一辆汽车有两道工序是 由机器人完成的.其一是紧固3只螺栓,其二是 焊接2处焊点.以X表示螺栓紧固得不良的数 目,以Y表示焊点焊接得不良的数目.据积累的 资料知(X,Y)具有分布律: 0 1 2 3 P(Y=j 0 0.840 0.030 0.020 0.010 0.900 1 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P{X=训 0.910 0.045 0.032 0.013 1.000
X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 2 0.010 0.005 0.004 0.001 1 0 0.900 0.080 0.020 P{X i} 0.910 0.045 0.032 0.013 1.000 P{Y j} ( , ) : , . 2 . . 3 , , 资料知 具有分布律 目 以 表示焊点焊接得不良的数目 据积累的 焊接 处焊点 以 表示螺栓紧固得不良的数 由机器人完成的 其一是紧固 只螺栓 其二是 在一汽车工厂中 一辆汽车有两道工序是 X Y Y X 例1
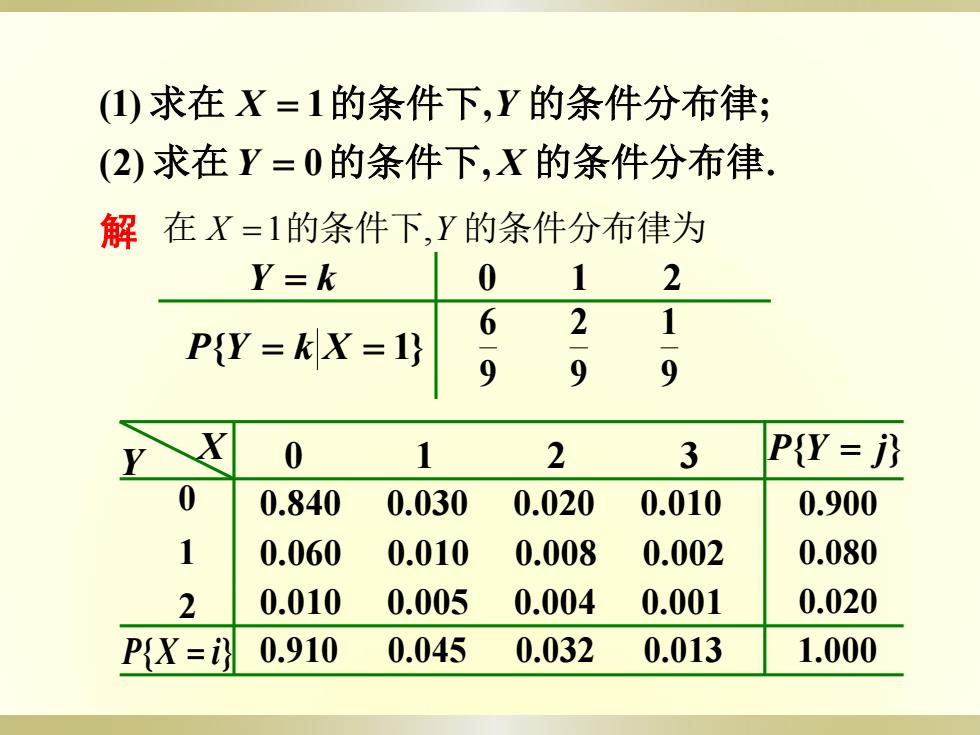
(1)求在X=1的条件下,Y的条件分布律; (2)求在Y=0的条件下,X的条件分布律. 解在X=1的条件下,Y的条件分布律为 Y=k 0 1 2 2 1 P(Y=kX=1) 9 9 9 0 1 2 3 P{Y=} 0.840 0.030 0.020 0.010 0.900 0.060 0.010 0.008 0.002 0.080 2 0.010 0.005 0.004 0.001 0.020 P{X=} 0.910 0.045 0.032 0.013 1.000
(2) 0 , . (1) 1 , ; 求在 的条件下 的条件分布律 求在 的条件下 的条件分布律 Y X X Y 解 X Y 0 1 2 3 0.840 0.030 0.020 0.010 0.060 0.010 0.008 0.002 2 0.010 0.005 0.004 0.001 1 0 0.900 0.080 0.020 P{X i} 0.910 0.045 0.032 0.013 1.000 P{Y j} 在 X 1的条件下,Y 的条件分布律为 Y k P{Y k X 1} 0 1 2 9 1 9 2 9 6