《概率论与数理统计》课程教学课件（PPT讲稿，48学时）第三章 多维随机变量及其分布 第四节 相互独立的随机变量

概率论与故理统外 第四节 相互被丘的随机变量

第四节 相互独立的随机变量

概率论与数理统外 1.定义 设F(x,y)及Fx(x),F,(y)分别是二维随机变量 (X,Y)的分布函数及边缘分布函数.若对于所有x,y 有 P{X≤x,Y≤y}=P{X≤xP{Y≤y, 即 F(x,y)=Fx(x)Fy(y), 则称随机变量X和Y是相互独立的

. ( , ) ( ) ( ), { , } { } { }, ( , ) . , ( , ) ( ), ( ) 则称随机变量 和 是相互独立的 即 有 的分布函数及边缘分布函数 若对于所有 设 及 分别是二维随机变量 X Y F x y F x F y P X x Y y P X x P Y y X Y x y F x y F x F y X Y X Y       1.定义

概率论与敖理统计「 2.说明 ()离散型随机变量(X,Y)的联合分布律为 P{X=x,Y=yj}=p,i,j=1,2,. X和Y相互独立 P(X=xi,Y=y=P(X=x)P(Y=y, 即P=P.P

 { , } { } { } , i j i j P X  x Y  y  P X  x P Y  y X 和 Y 相互独立 2.说明 (1) 离散型随机变量 ( X,Y )的联合分布律为 P{X  x ,Y  y }  p , i, j 1,2,  . i j i j pij pi p j 即  

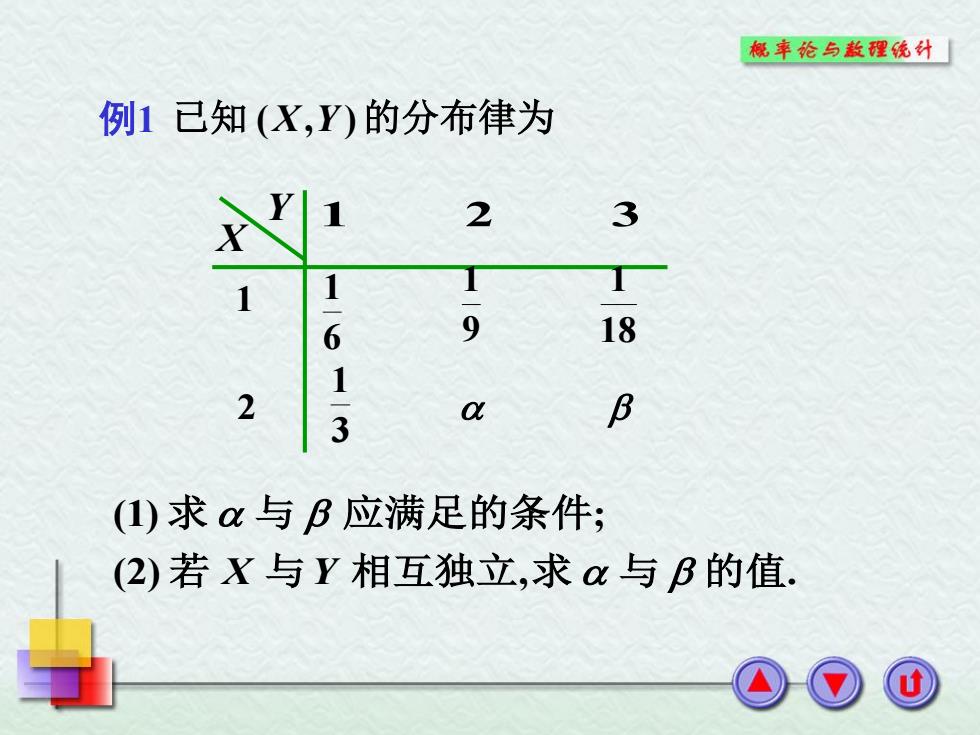
概率论与数理统外「 例1已知(X,Y)的分布律为 2 3 T 1 1 6 -9 18 1 2 3 a B ()求与B应满足的条件； (2)若X与Y相互独立，求α与B的值

例1 已知 (X,Y )的分布律为 (2) , . (1) ; 若 与 相互独立 求 与 的值 求 与 应满足的条件     X Y 1 2 1 2 3 6 1 9 1 18 1 3 1   X Y

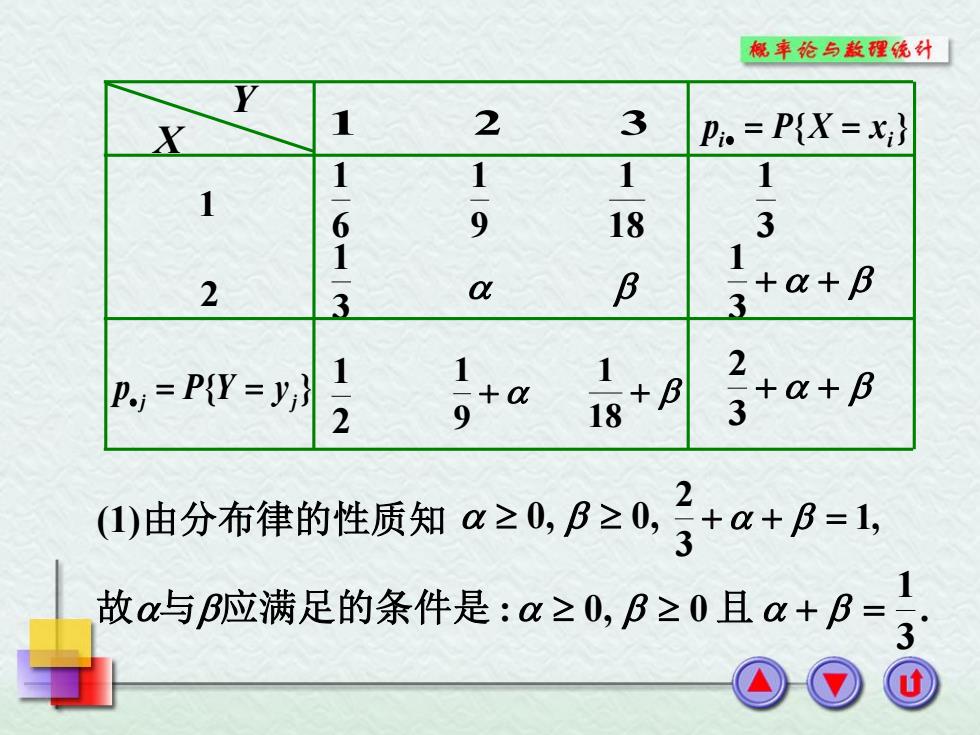
概率论与敖理统计「 1 2 3 Pi.P(X=x} 1 1 1 1 1 6 9 18 3 1 1 2 3 a B 2+a+B 3 卫=PW=y, 1-2 1 3+a+B (由分布律的性质知a≥0B≥0号+a+A=1 故a与应满足的条件是：a≥0，B≥0且a+B= 3

(1)由分布律的性质知   0,   0, 1, 3 2     . 3 1 故与应满足的条件是 :  0,   0 且    X Y 1 2 3 1 2 6 1 9 1 18 1 3 1   { } i i p  P X  x  3 1    3 1 { } j j p  P Y  y  2 1  9 1   18 1    3 2