
导航 解:(1).函数y=l0g2x在区间(0,+o)内是增函数,π>0.9, 10g2>l0g20.9. (2).10g20.3<l0g21=0,l0g0.20.3>l0g0.21=0, ∴l0g20.3<l0g0.20.3. (3).60.7>60=1,l0g0.76<10g0.71=0, ∴.60.7>l0g0.76
导航 解:(1)∵函数y=log2x在区间(0,+∞)内是增函数,π>0.9, ∴log2π>log20.9. (2)∵log20.3<log21=0,log0.20.3>log0.21=0, ∴log20.3<log0.20.3. (3)∵6 0.7>6 0=1,log0.76<log0.71=0, ∴6 0.7>log0.76
导航 (4)(解法一)函数=l0g2和y=l0g3x的图象如图所示,当x>1 时y=l0g2x的图象在y=l0g3x的图象上方,这里x=5, .l0g25>l0g35. y=log2x (解法)rog5之lg5 y=log3x 又l0gs3>l0gs2>0, 5 .l0gz5>l0g35
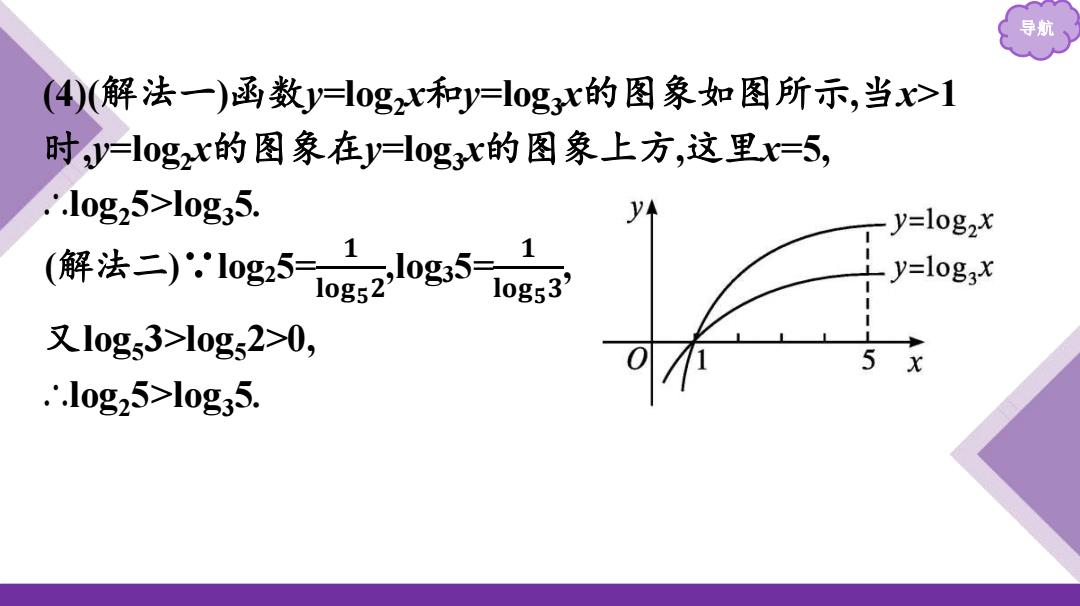
导航 (4)(解法一)函数y=log2x和y=log3x的图象如图所示,当x>1 时,y=log2x的图象在y=log3x的图象上方,这里x=5, ∴log25>log35. (解法二)∵log25= 𝟏 𝐥𝐨𝐠𝟓 𝟐 ,log35= 𝟏 𝐥𝐨𝐠𝟓 𝟑 , 又log53>log52>0, ∴log25>log35

导航 反思感悟比较对数大小的方法 类型 方法 底数相同,真数不同 利用对数函数的单调性 底数不同,真数相同 1.化为同底数;2.利用图象 底数不同,真数不同 利用中间量 指数值与对数值的比较 利用中间量
导航 反思感悟 比较对数大小的方法 类 型 方 法 底数相同,真数不同 利用对数函数的单调性 底数不同,真数相同 1.化为同底数;2.利用图象 底数不同,真数不同 利用中间量 指数值与对数值的比较 利用中间量