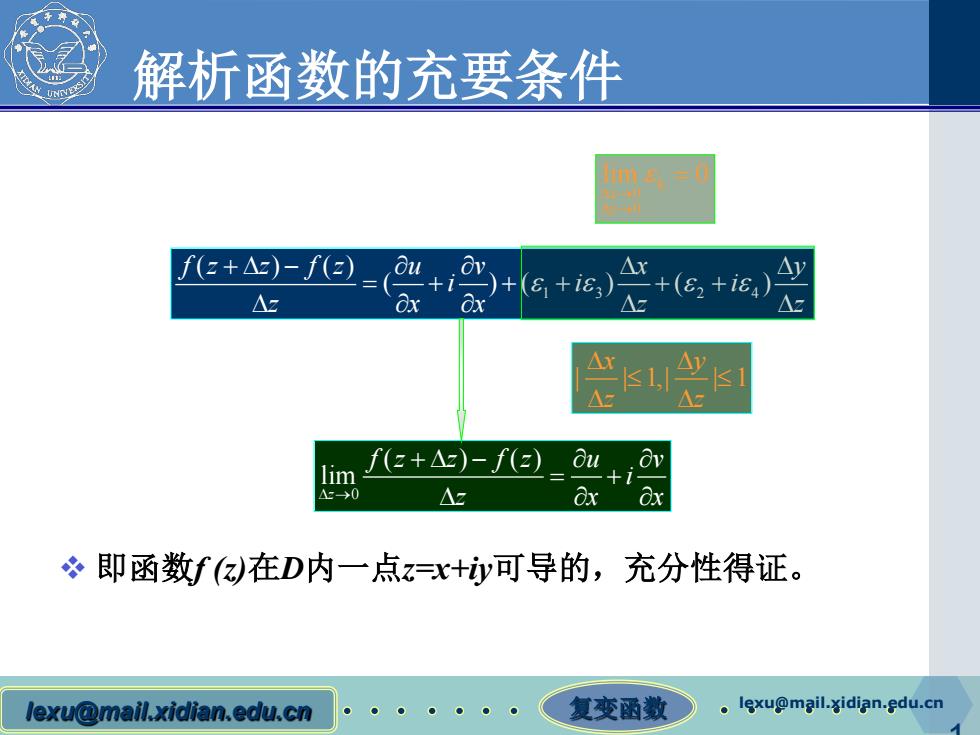
解析函数的充要条件 +A9)-但-0+)+lG+i,)A+(e,+ia,)义 △z f(z+△)-f(z)ou,. lim +1 △2-→0 △z Ox 即函数f在D内一点z=x+y可导的,充分性得证。 lexu@mail.xidian.edu.cn ●● 复变函数 .lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 1 解析函数的充要条件 即函数f (z)在D内一点z=x+iy可导的,充分性得证。 13 24 ( ) () ( )( ) ( ) fz z fz u v x y ii i z xx z z εε εε +∆ − ∂ ∂ ∆ ∆ = + ++ ++ ∆ ∂∂ ∆ ∆ | | 1,| | 1 x y z z ∆ ∆ ≤ ≤ ∆ ∆ k 0 0 lim 0 x y ε ∆ → ∆ → = 0 ( ) () lim z fz z fz u v i ∆ → z xx +∆ − ∂ ∂ = + ∆ ∂∂
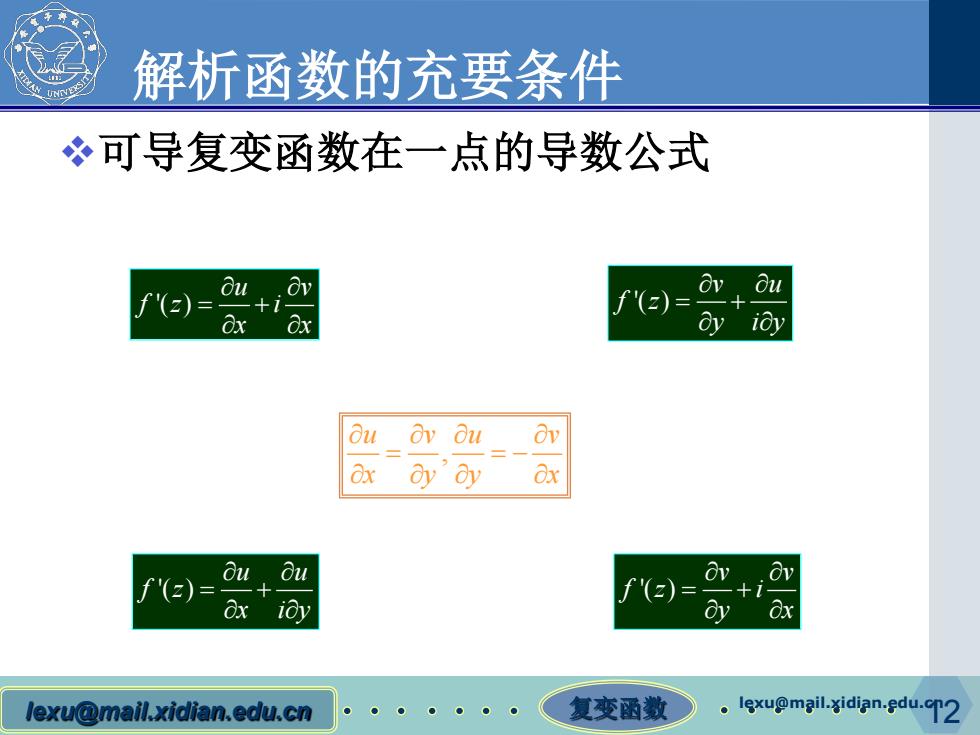
解析函数的充要条件 冬可导复变函数在一点的导数公式 o 0+i Ov Ou f'(z)= Oy ioy ou a dy'dy f八(z)=+ 8x f(z)=。+ia ioy Oy Ox lexu@mail.xidian.edu.cn 复变函数 。lexu@mgil-¥idian..edu.cT2
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn12 解析函数的充要条件 可导复变函数在一点的导数公式 '( ) u v fz i x x ∂ ∂ = + ∂ ∂ , u vu v x yy x ∂ ∂∂ ∂ = = − ∂ ∂∂ ∂ '( ) v u f z y iy ∂ ∂ = + ∂ ∂ '( ) u u f z x iy ∂ ∂ = + ∂ ∂ '( ) v v fz i y x ∂ ∂ = + ∂ ∂

解析函数的充要条件 冬函数在区域D内解析的充要条件 ·函数f()=uc)+iK)在区域D内 ·u(化,y)和v化,y)在区域D可微 ·且在区域D满足柯西黎曼方程 [推论若函数f)在区域D内满足C-R方程, 且u化,)、v化,y)具有一阶连续偏导 数,则函数f在区域D内解析。 lexu@mail.xidian.edu.cn 复变函数 lexu@mgil.xidian.edu.cn
lexu@mail.xidian.edu.cn 复变函数 lexu@mail.xidian.edu.cn 1 解析函数的充要条件 函数在区域D内解析的充要条件 函数f (z)= u(x,y)+i v(x,y)在区域D内 u(x,y)和v(x,y)在区域D可微 且在区域D满足柯西-黎曼方程 [推论]若函数f (z)在区域D内满足C-R方程, 且u (x, y)、v (x, y)具有一阶连续偏导 数,则函数f (z)在区域D内解析