(3)指出②⑤⑥中函数的单调性 导航 提示: 单调区间 (-00,0) (0,+oo) ②fx)=x 增函数 增函数 ⑤fx)=x3 增函数 增函数 @w日 减函数 减函数 (4)总结问题(2)3)的答案,你能得到什么一般性的结论? 提示:偶函数在x<0与x>0时的单调性是相反的,奇函数在x<0 与x>0时的单调性是相同的
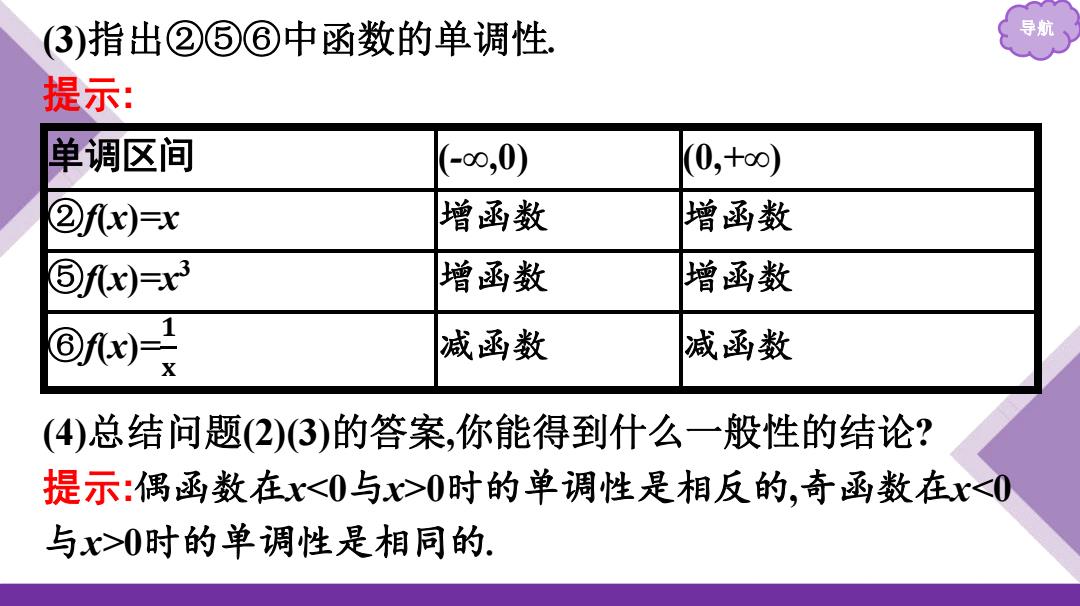
导航 (3)指出②⑤⑥中函数的单调性. 提示: 单调区间 (-∞,0) (0,+∞) ②f(x)=x 增函数 增函数 ⑤f(x)=x3 增函数 增函数 ⑥f(x)= 𝟏 𝐱 减函数 减函数 (4)总结问题(2)(3)的答案,你能得到什么一般性的结论? 提示:偶函数在x<0与x>0时的单调性是相反的,奇函数在x<0 与x>0时的单调性是相同的

导航 2.填空:(1)如果函数y=fx)是偶函数,那么其在区间[,b]与[-b, -(或(-o,0)与(0,+∞)上的单调性 (2)如果函数y=fx)是奇函数,那么其在区间[a,b]与-b,-(或 (-o,0)与(0,+∞)上的单调性
导航 2.填空:(1)如果函数y=f(x)是偶函数,那么其在区间[a,b]与[-b, -a](或(-∞,0)与(0,+∞))上的单调性相反. (2)如果函数y=f(x)是奇函数,那么其在区间[a,b]与[-b,-a](或 (-∞,0)与(0,+∞))上的单调性相同

导航 3.做一做:(1)已知定义在R上的偶函数y=fx)在区间(0,+o)内 单调递增,则1)与f孔3)的大小关系是 (2)已知y=fx)是定义在R上的奇函数,且在区间(-o,0)内单调 递减.若fc-1)>f1),则x的取值范围是
导航 3.做一做:(1)已知定义在R上的偶函数y=f(x)在区间(0,+∞)内 单调递增,则f(-1)与f(-3)的大小关系是 . (2)已知y=f(x)是定义在R上的奇函数,且在区间(-∞,0)内单调 递减.若f(x-1)>f(1),则x的取值范围是

导航 解析:1)(方法一)因为y=fx)在区间(0,+o)内单调递增,且y= 是偶函数,所以y=x)在区间(oo,0)内单调递减,所以孔-1)<-3), (方法二)因为y=f)是偶函数,所以-1)=1)几-3)=f3). 又y=fx)在区间(0,+o)内单调递增, 所以1)f3),即-1)f孔-3). (2)由题意可知函数y=fx)在R上单调递减, 所以不等式fx-1)>f1)等价于x1<1,解得x<2. 答案:(1)f-1)f-3)(2)(-o,2)
导航 解析:(1)(方法一)因为y=f(x)在区间(0,+∞)内单调递增,且y=f(x) 是偶函数,所以y=f(x)在区间(-∞,0)内单调递减,所以f(-1)<f(-3). (方法二)因为y=f(x)是偶函数,所以f(-1)=f(1),f(-3)=f(3). 又y=f(x)在区间(0,+∞)内单调递增, 所以f(1)<f(3),即f(-1)<f(-3). (2)由题意可知函数y=f(x)在R上单调递减, 所以不等式f(x-1)>f(1)等价于x-1<1,解得x<2. 答案:(1)f(-1)<f(-3) (2)(-∞,2)

二、函数图象的对称性 导航 【问题思考】 1,已知二次函数fx)=x24x, (1)函数x)=x24x图象的对称轴是什么? 提示:直线x=2 (2)对任意的实数h,是否都有f2-)=f2+)成立? 提示:是, (3)若函数y=g(c)对任意的实数,都有g(2-h)=g(2+h),则y=g8 的图象的对称轴是什么? 提示:直线x=2
导航 二、函数图象的对称性 【问题思考】 1.已知二次函数f(x)=x2 -4x, (1)函数f(x)=x2 -4x图象的对称轴是什么? 提示:直线x=2. (2)对任意的实数h,是否都有f(2-h)=f(2+h)成立? 提示:是. (3)若函数y=g(x)对任意的实数h,都有g(2-h)=g(2+h),则y=g(x) 的图象的对称轴是什么? 提示:直线x=2