
第华章 导数与微分 高等数学少学时 例1设y=x2,当r=2,△x=0.01时,求△y,y及△y-d. 解y=(x2)'d=2xdc, Ay=(x+△x}-x2=2xAx+(△x}. ∴.当r=2,△x=d=0.01时, Ay,=2xAc+acl3=2-20.01+0.01y=0.0401, c=0.01 ..dy2=2xA 2=2.2.0.01=0.04, △x=0.01 △x=0.01 (4y-4w)g21=0.0401-0.04=0.001 北京邮电大学出版社 6
6 例 1 2, 0.01 , . 2 设 y = x , 当x = x = 时,求y dy及y − dy ( ) 2 , 2 dy = x dx = xdx 当x = 2,x = dx = 0.01时, 2 0.01 2 0.01 2 == = = = xx x dy x x x 解 ( ) 2 ( ) . 2 2 2 y = x + x − x = xx + x ( ) 0.0 1 2 2 0.0 1 2 2 == = = = + xx x y x x x x 2 2 0.01 (0.01 ) 0.0401, 2 = + = = 2 2 0 .01 = 0 .04 , ( ) 0 .01 2 = − =x y dy x = 0.0401 − 0.04 = 0.0001
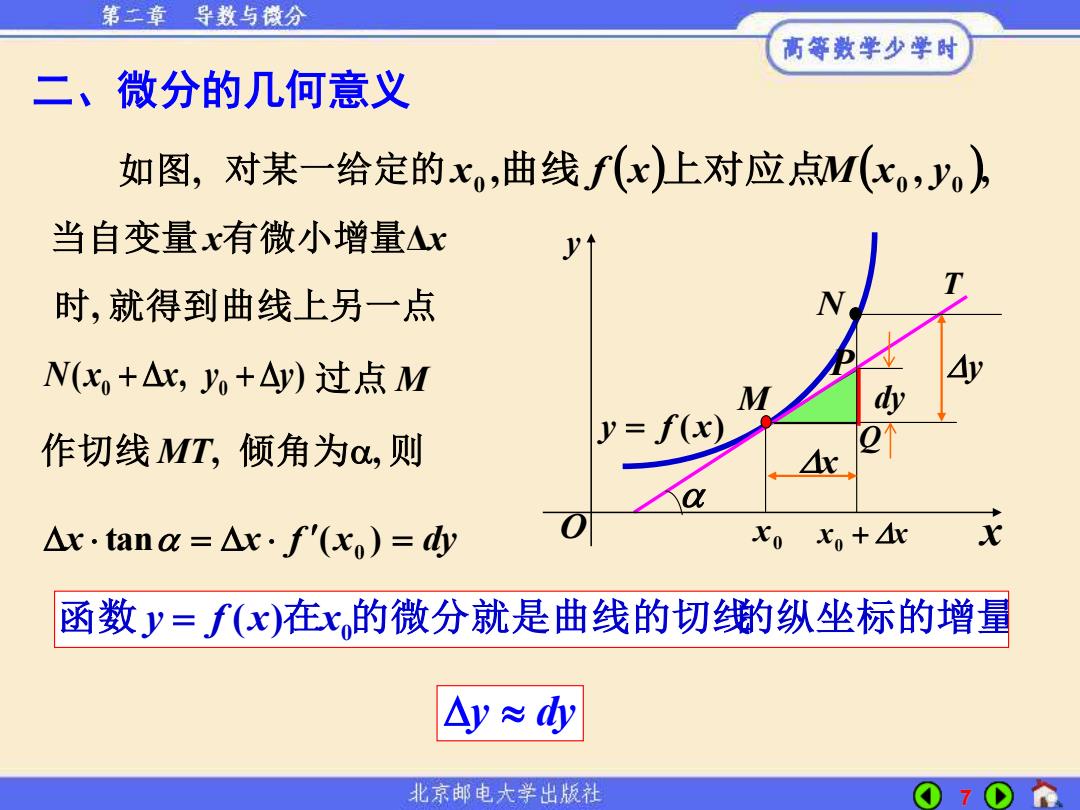
第三章导数与微分 高等数学少学时 二、微分的几何意义 如图,对某一给定的x,曲线f(x)上对应点M(xoy) 当自变量x有微小增量△x 时,就得到曲线上另一点 N(x,+△x,y+△y)过点M M 作切线MT,倾角为o,则 y=f(x) △x·tana=x·f'(xo)=y x0x。+ x 函数y=f(x)在x的微分就是曲线的切线的纵坐标的增量 △y≈ 北京邮电大学出版社
7 二、微分的几何意义 ( , ) 0 0 N x + x y + y 作切线 MT, 倾角为, 则 时, 就得到曲线上另一点 当自变量 x有微小增量Δx 如图, , ( ) ( , ), 0 0 0 对某一给定的 x 曲线 f x 上对应点M x y tan ( ) x0 x = x f = dy 函 数 y = f (x)在x0 的微分就是曲线的切线的纵坐标的增量 y dy 过点 M y = f (x) M N Q T P x y dy x + x 0 0 x x y O