
2.不定积分的定义:在区间I内,函数f(x)的带有任意常数项的原函数称为f(x)在区间I内的不定积分记为[ f(x)dx.f(x)dxF(x)+C被积表达式被积函数任意常数积分号积分变量
任 意 常 数 积 分 号 被 积 函 数 2.不定积分的定义: f (x)dx = F(x) + C 被 积 表 达 式 积 分 变 量 , ( ) ( ) ( ) . I f x f x I f x dx 在区间 内 函数 的带有任意常数项的 原函数称为 在区间 内的不定积分, 记为

例1 求dx.2+X解:(arctanx):1+x?dx = arctanx + C.2+X11-dx例2 求x解: 当x>0时,(ln x) =二, : 在(0,+o0)内1dx=Inx+Cx当x<0时,(ln(-x)=二,: 在(00,0)内,=d-dx=In(-x)+CXX1-dx = In |x|+ C.综合:x
例2 求 1 dx. x 解: 1 x x 0 (ln ) , x 当 = 时, 1 dx x C ln . x = + 综合: 2 1 (arctan ) , 1 x x = + arctan . 1 1 2 = + + dx x C x 1 (0, ) ln dx x C x + = + 在 内, 1 x x 0 (ln( )) , x 当 − = 时, 1 ( ,0) ln( ) dx x C x − = − + 在 内, 解 例1 求 . 1 1 2 + dx x

例3设曲线通过点(1,2),且其上任一点处的切线斜率等于这点横坐标的两倍,求此曲线方程设曲线方程为y=f(x)解dy根据题意得= 2x,dx即f(x)是2x的一个原函数,: J2xdx =x +C,. f(x) = x2 +C,由曲线通过点(1,2) →> C =1,所求曲线方程y=x2+1
例3 设曲线通过点(1,2),且其上任一点处的切线 斜率等于这点横坐标的两倍,求此曲线方程. 解 设曲线方程为y f x = ( ), 2 , dy x dx 根据题意得 = 2 , 2 xdx = x + C ( ) , 2 f x = x + C 由曲线通过点(1,2) C = 1, 2 所求曲线方程 1. y x = + 即f x x ( ) 2 是 的一个原函数
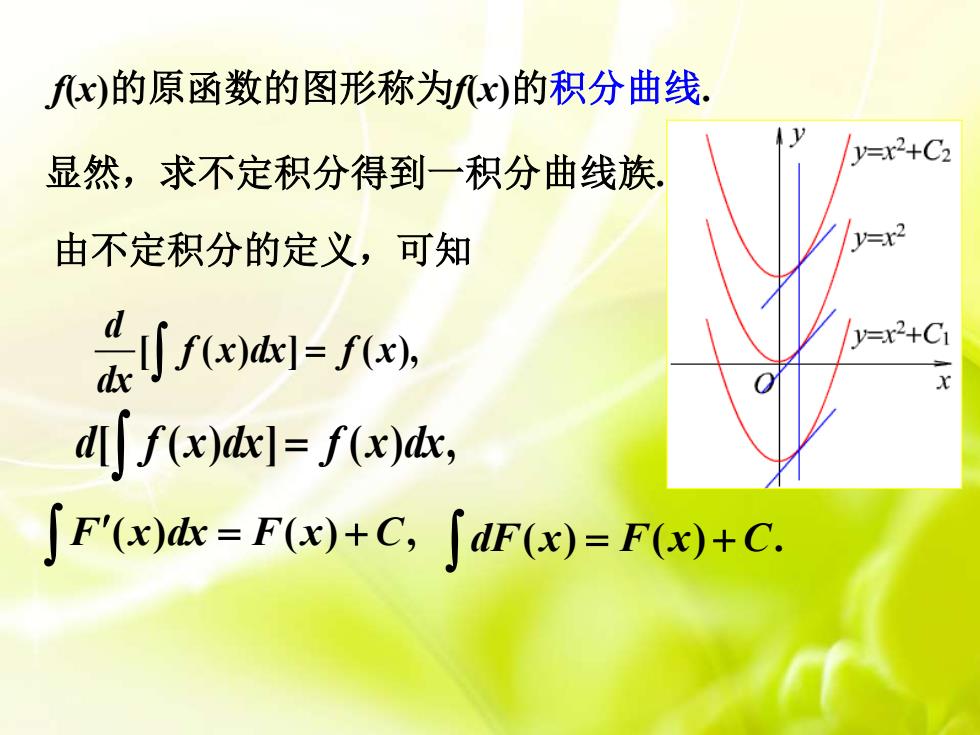
f(x)的原函数的图形称为f(x)的积分曲线V=x2+C2显然,求不定积分得到一积分曲线族y=x2由不定积分的定义,可知y=x2+Ci (x)tl= (x),xdlf f(x)dx)= f(x)dx,[ F'(x)dx = F(x)+C, [dF(x)= F(x)+C
显然,求不定积分得到一积分曲线族. 由不定积分的定义,可知 [ ( ) ] ( ), d f x dx f x dx = d[ f (x)dx] = f (x)dx, ( ) ( ) , F x dx = F x + C ( ) ( ) . dF x = F x + C f(x)的原函数的图形称为f(x)的积分曲线

>说明:1.被积函数是原函数的导数.被积表达式是原函数的微分2.不定积分表示那些导数等于被积函数的所有函数.或说其微分等于被积表达式的所有函数.因此绝不能漏写积分常数C3.求已知函数的原函数或不定积分的运算称为积分运算,它是微分运算的逆运算
1. 被积函数是原函数的导数,被积表达式是 原函数的微分. 2. 不定积分表示那些导数等于被积函数的所 有函数.或说其微分等于被积表达式的所有 函数.因此绝不能漏写积分常数C. 3. 求已知函数的原函数或不定积分的运算称 为积分运算,它是微分运算的逆运算. ➢ 说明: