《线性代数》课程教学课件（PPT讲稿，A）5-2 方阵的特征值与特征向量

线性代数第五卖（解(A-2E)X=0对 = 2,[3-2-11X1[=0(A-2E)x =-1 3-2//x,X基础解系：P=(1，1),：: Pi =(1,1)为属于特征值2的一个特征向量,其全部特征向量为kpi（k≠0);同理可求属于孔,=4的一个特征向量为 2=(-1,1)其全部特征向量为p2(k ±0)

线性代数 第五章 2, 对1 = 1 2 3 2 1 ( 2 ) 1 3 2 x A E x x   − −   − =      − −   下边求特征向量( ) 解( ) A E X O − = 2 0 ; 其全部特征向量为kp1 （k  ） 1  = 基础解系: (1 1) p ，  ， 1  = p (1, 1) 2 , 为属于特征值 的一个特征向量 1 2 1 1 0 0 0 x x   −     =      即 = 2 2 同理可求属于 = = − 4 ( 1 1) , 的一个特征向量为 p ，  ( 0). 其全部特征向量为kp2 k 

线性代数 第五幸求特征值与特征向量的步骤1.解A-aE=0求出a的值，即求特征值；2. 对每一个入,求方程组(A-2E)x=0的基础解系，即得到属于这个特征值的线性无关的特征向量n-R(A-E)个

线性代数 第五章 1. 0 , 解 A E − =   求出 的值 即求特征值； 2. , ( ) A E O x  − =  对每一个 求方程组 的基础解系， 求特征值与特征向量的步骤： n –R(A–λE)个 即得到属于这个特征值的线性无关的特征向量

线性代数 第五享01-1例2 求矩阵A=的特征值和特征向量-430A的特征多项式为解0-1-2103-2A-E==(2 - 2)(1- 2)2-402-2所以A的特征值为i = 2,2= 3 =1

线性代数 第五章 1 1 0 4 3 0 . 1 0 2 2 A   −   = −       例 求矩阵 的特征值和特征向量 解 2 1 1 0 4 3 0 (2 )(1 ) , 1 0 2 A A E       − − − = − − = − − − 的特征多项式为 2, 1. 所以A的特征值为1 = 2 = 3 =

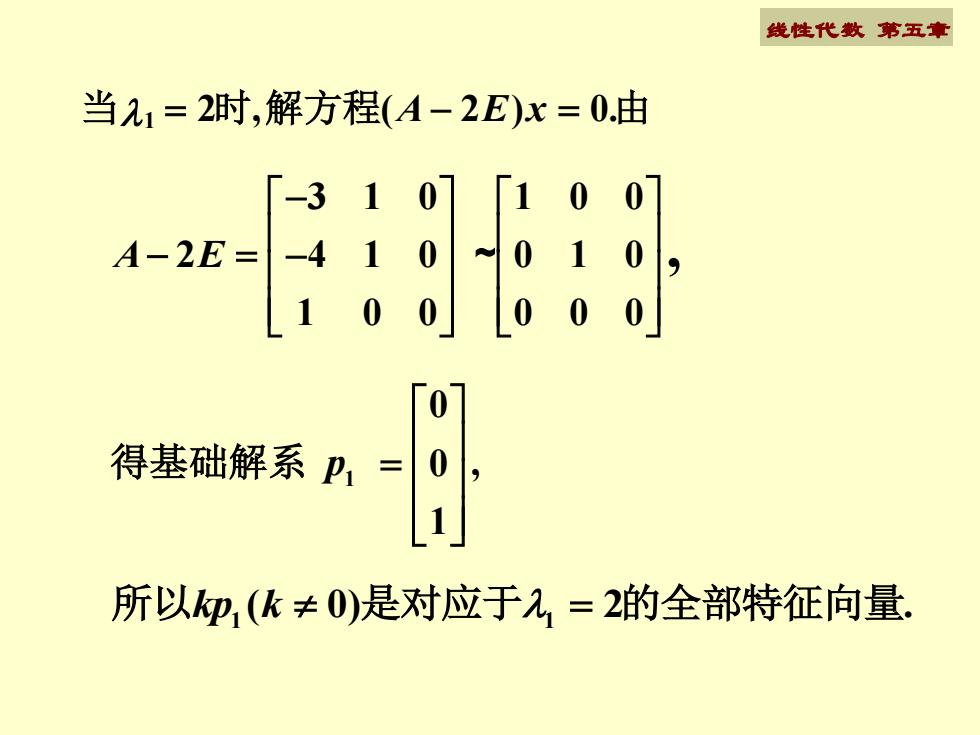
线性代数第五卖当a1=2时,解方程(A-2E)x=0.由A-2E=0得基础解系 Pi=所以kp(k0)是对应于a,=2的全部特征向量

线性代数 第五章 1 0 , 0 1 p     =       得基础解系 1 1 所以kp k( 0) 2 .  = 是对应于 的全部特征向量 当1 = 2时,解方程(A − 2E)x = 0.由 3 1 0 1 0 0 2 4 1 0 0 1 0 1 0 0 0 0 0 A E ,     −     − = −             ~

线性代数第五卖当22= 23=1时,解方程(A-E)x= 0.由A-E=得基础解系 Pz=-2所以kpz(k±0)是对应于,=,=的全部特征向量

线性代数 第五章 2 1 2 , 1 p   −   = −       得基础解系 2 2 3 所以kp k( 0) 1 .  = = 是对应于  的全部特征向量 当2 = 3 = 1时,解方程(A − E)x = 0.由 2 1 0 1 0 1 4 2 0 0 1 2 , 1 0 1 0 0 0 A E     −     − = −             ~