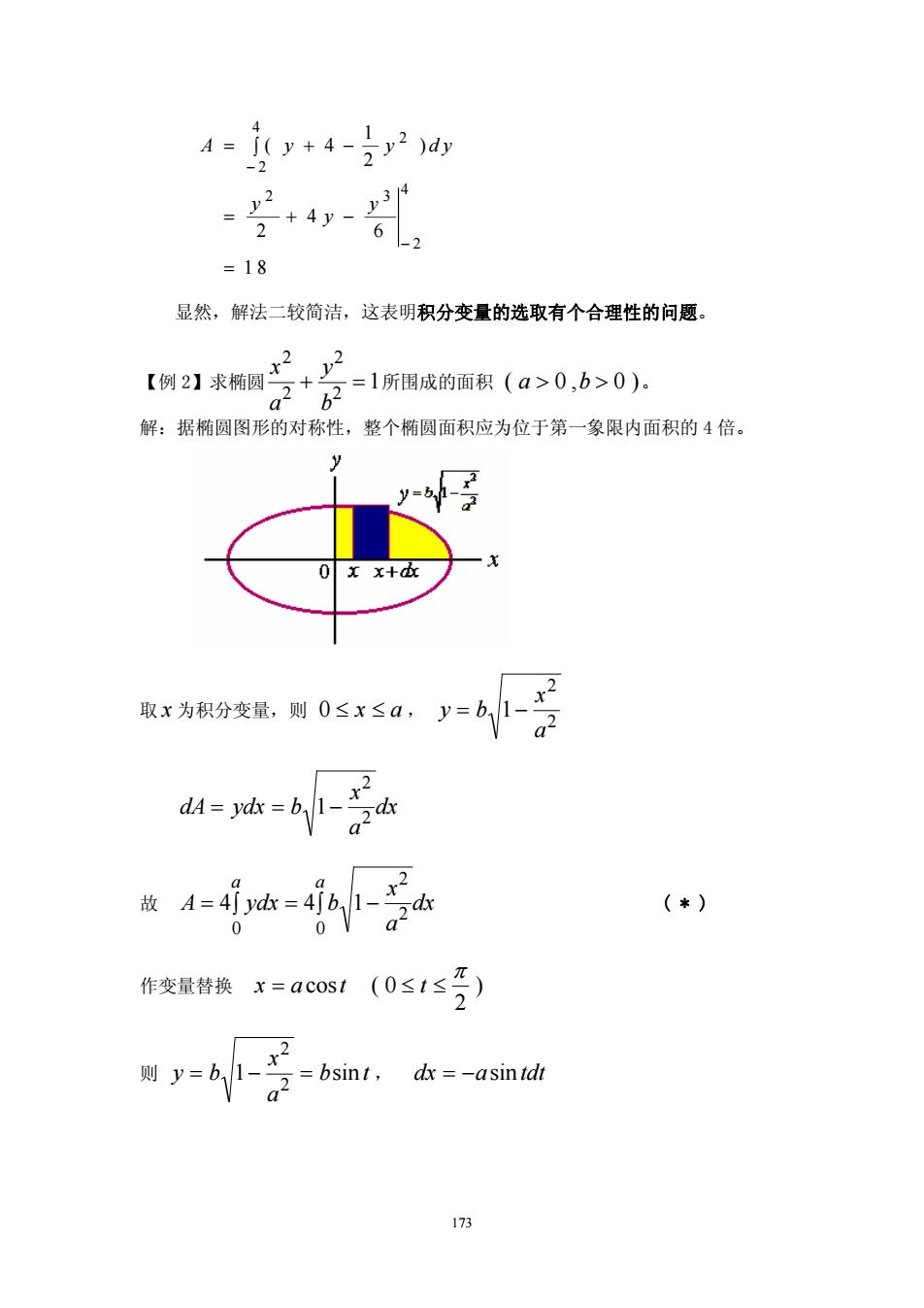
412J( y+ 4A=)dyV2-2,3 /4y=+4V26-2= 18显然,解法二较简洁,这表明积分变量的选取有个合理性的问题。22=1所围成的面积(a>0,b>0)。【例2】求椭圆2+62a解:据椭圆图形的对称性,整个椭圆面积应为位于第一象限内面积的4倍。yV=b,h2x0xx+dx取x为积分变量,则0≤x≤a,y=bldA = ydx =dxORaa4[badx故A= 4J ydx:(*)O00元(0≤t≤作变量替换x=acost2bbsint,dx =-asintdt则y==2a173
173 A y y dy y y y = +− ∫ = +− = − − ( ) 4 1 2 2 4 6 1 8 2 4 2 2 3 2 4 显然,解法二较简洁,这表明积分变量的选取有个合理性的问题。 【例 2】求椭圆 x a y b 2 2 2 2 + = 1所围成的面积 ( ,) a b > > 0 0 。 解:据椭圆图形的对称性,整个椭圆面积应为位于第一象限内面积的 4 倍。 取 x 为积分变量,则 0 ≤ ≤ x a , y b x a = −1 2 2 dA ydx b x a ==−1 dx 2 2 故 A ydx b x a dx a a = 4 41 ∫ = − ∫ 0 2 2 0 ( * ) 作变量替换 x a = cost ( ) 0 2 ≤ ≤t π 则 y b x a = −= 1 b t 2 2 sin , dx a td = − sin t

0(**)A = 4J(bsint)(-asint)dt元2K12=4abj sin dt =4ab.-1= maob22!!0例:从抛物线y=x2-1上的点P引抛物线y=x的切线,证明该切线与y=x?所围成的面积与P点的位置无关解:设Q(x,),Q(x2,y2)分别表示从点P(xo,%)向抛物线y=x2引出的两条切线的切点.y=x2在点9(x,J)的切线方程y-y=2x(x-x)即y-x =2x(x-x)又= x -1= x =x +1,x = x -1于是切线PQ,PQ,的方程分别为y = 2(x + 1)x-(x +1)y= 2(x -1)x-(x。 -1)2由y=x,P9,及PQ,所围图形的面积为A = [ [x - 2(x0 -1)x+(x -1)]dx+[* [x? -2(xo +1)x+(x +1)"]dx 可见A与x无关,A与点P(x%)位置无关x21与直线x=-V3,x=V3围成的图形面积例:求曲线y=2J1+xy解:两曲线交点为(1,).由于图形关于y轴对称1V5x2x).dx+故A::d1+x21+.3n174
174 A b t a t dt = − 4 ∫ 2 0 ( sin )( sin ) π ( * * ) ab tdt ab πab π π ⋅ = − = = ⋅ ∫ 2!! 2 (2 1)!! 4 sin 4 2 0 2 例: 2 2 从抛物线 上的点 引抛物线 的 y =− = x P yx 1 2 切线 证明该切线与 所围成 , y x = 的面积与 点的 P 位置无关. 解:设 111 2 2 2 Qxy Qx y ( , ), ( , ) 分别表示从点 0 0 Px y (, )向抛物线 2 y = x 引出的两条切线 的切点. 2 y = x 在点 111 Qxy (, )的切线方程: 11 1 y −= − y xx x 2( ) 即 2 0 1 10 1 y x xx x −= − 2( ) 又 2 00 10 10 yx xx xx = −⇒ = + = − 1 1, 1 于是切线 1 2 PQ PQ , 的方程分别为 2 0 0 y x xx = +−+ 2( 1) ( 1) 2 0 0 y x xx = −−− 2( 1) ( 1) 2 1 2 由 及 y x PQ PQ = , 所围图形的面积为 0 0 0 0 1 2 22 2 00 00 1 [ 2( 1) ( 1) ]d [ 2( 1) ( 1) ]d x x x x A x x xx x x x xx x + − = − −+− + − +++ ∫ ∫ 2 . 3 = 可见 A x 与 无关 0 , 0 0 A Px y 与点 (, ) 位置无关 例: 2 2 1 , 3, 2 1 x yy x x = = =− + 求曲线 与直线 x = 3 . 围成的图形面积 解:两曲线交点为 1 1 (1, ),( 1, ). 2 2 − 由于图形关于 y 轴对称, 故 2 2 1 3 2 2 0 1 1 1 2 ( )d 2 ( )d 1 2 21 x x Ax x x x = − ⋅+ − ⋅ + + ∫ ∫ − 3 3 O x y 2 1 1 y x = + 2 2 x y = − 1 1 1
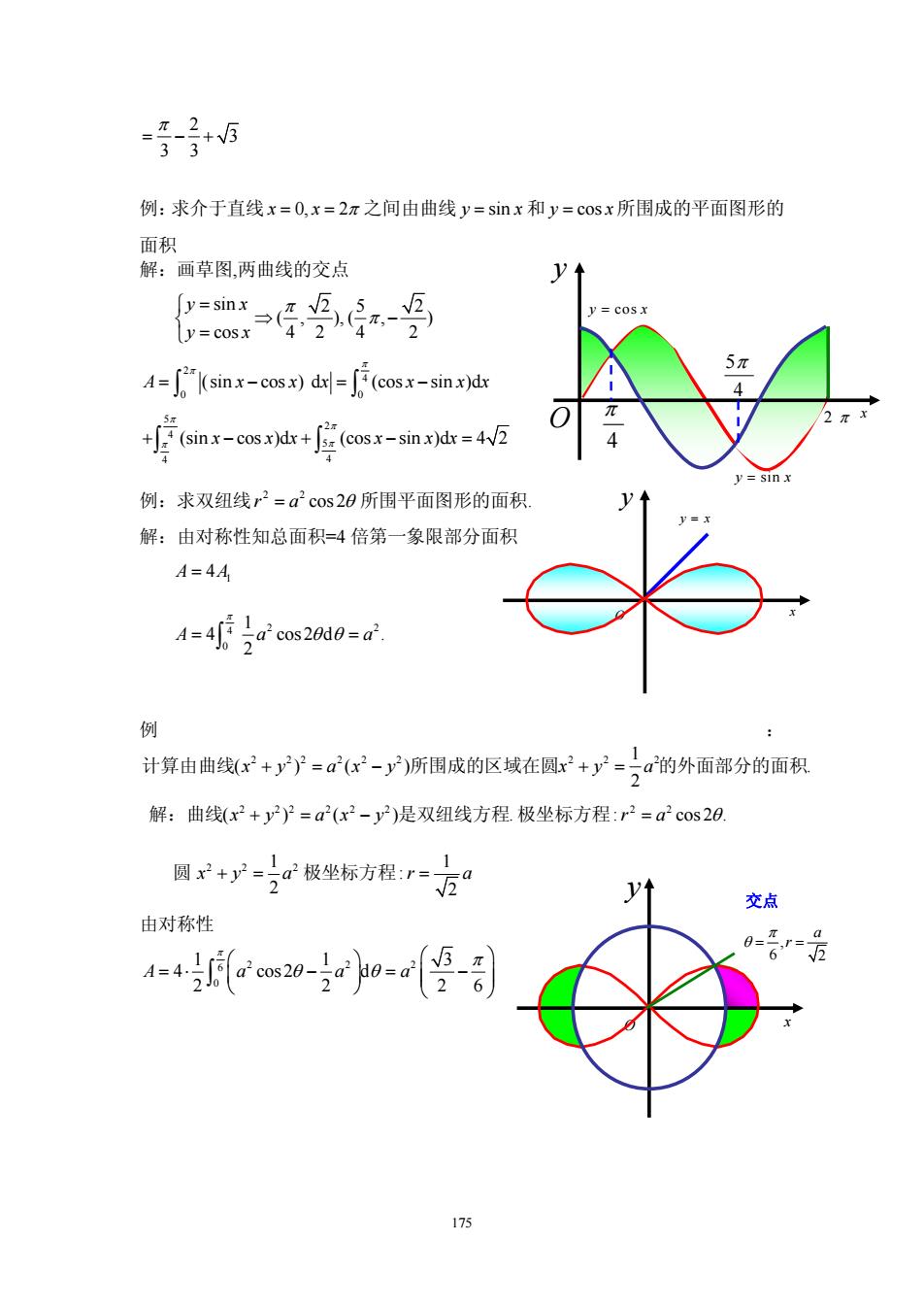
2+V333例:求介于直线x=0.x=2元之间由曲线y=sinx和y=cosx所围成的平面图形的面积解:画草图,两曲线的交点yt=sin(),V25y=cosx4GT4*ny=cosx5元2 (sin x-cos x) dx|= [(cosx-sin x)dx1=4元02元[ (sinx-cos x)dx+J(cosx-sin x)dx=4/24y=sinx例:求双纽线r?=αcos20所围平面图形的面积解:由对称性知总面积=4倍第一象限部分面积A=4A,a?cos20de=a?4=4L例计算由曲线(x2+)=α(x2-)所围成的区域在圆x2+α"的外面部分的面积2解:曲线(x+y2)=α(x2-y)是双纽线方程极坐标方程:r2=αcos21α极坐标方程:r=圆x+=CV2V交点由对称性0=2hacos20-d=a1=4.aOJ6175
175 2 3 3 3 π = −+ 例:求介于直线 x x = 0, 2 = π 之间由曲线 y = sin x 和 y = cos x所围成的平面图形的 面积 解:画草图,两曲线的交点 sin 25 2 ( , ), ( , ) cos 42 4 2 y x y x π π ⎧ = ⎨ ⇒ − ⎩ = 2 4 0 0 A x x x x xx (sin cos ) d (cos sin )d π π = − =− ∫ ∫ 5 2 4 5 4 4 (sin cos )d (cos sin )d 4 2 x xx x xx π π + −+ −= ∫ ∫ π π 例:求双纽线 2 2 r a = cos 2θ 所围平面图形的面积. 解:由对称性知总面积=4 倍第一象限部分面积 1 A A = 4 2 2 4 0 1 4 cos 2 d . 2 Aa a π = = θ θ ∫ 例 : 2 22 2 2 2 2 2 2 1 ( )( ) . 2 计算由曲线 所围成的区域在圆 的外面部分的面积 x y ax y x y a + = − += 解: 2 22 2 2 2 曲线 是双纽线方程 ( )( ) . x y ax y += − 2 2 极坐标方程: cos 2 . r a = θ 22 2 1 2 圆 x + = y a 1 : 2 极坐标方程 r a = 由对称性 2 22 6 0 1 13 4 cos 2 d 2 2 26 A a aa π π θ θ ⎛ ⎞ ⎛ ⎞ =⋅ − = − ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ∫ y x = cos y x = sin O x y 2 π 4 π 5 4 π y x = O x y , 6 2 a r π θ = = 交点 O x y

例:求界于二椭圆+xy2=1(a>b>0)之间图形面积=1b?b2aa'12x2解:所求面积A为在第一象限中由直线V=x,x轴及椭圆q2b2y所围图形面积的8倍x2y22x2=+b2将椭圆=1化为极坐标方程ab2Q2y=Xy2x=rcoso代入椭圆26y=rsingaxa’b2得2=4r2(0)d0,A=8.Va”cos?+b’sin?g2J0y=x1[3r(0)d = 4a2b [A=8.dea?cos?+b?sin?16d= 4ab-tanの)ab2b2acos e(1+tantan?0)1+aab=4abarctan(a极坐标情形二、设平面图形是由曲线r=β()及射线=α,=β所围成的曲边扇形。β0+doAA=r()d75取极角θ为积分变量,则α≤θ≤β,在平面图形中任意截取一典型的面积元素△A,它是极角变化区间为[0,0+dO]的窄曲边扇形。△A的面积可近似地用半径为r=(の),中心角为dO的窄圆边扇形的面积来代替,即176
176 例: 22 22 22 22 1, 1( 0) xy xy a b ab ba 求界于二椭圆 之间图形面积 + = + = >> . 解:所求面积 A 为在第一象限中由直线 y x = , x 轴及椭圆 2 2 2 2 1 x y b a + = 所围图形面积的 8 倍. 将椭圆 2 2 2 2 1 x y b a + = 化为极坐标方程. 将 cos sin x r y r θ θ ⎧ = ⎨ ⎩ = 代入椭圆 2 2 2 2 1, x y b a + = 得 2 2 2 2 4 2 2 22 0 1 , 8 ( )d cos sin 2 a b r Ar a b π θ θ θ θ = =⋅ + ∫ 2 22 4 4 2 2 22 0 0 1 1 8 ( )d 4 d 2 cos sin A r ab a b π π θ θ θ θ θ =⋅ = + ∫ ∫ 2 4 2 0 2 2 2 1 4 d cos (1 tan ) b b a π θ θ θ = + ∫ 4 2 0 2 2 1 4 ( tan ) 1 tan b ab d b a a π θ θ = + ∫ 4 arctan( ) b ab a = 二、 极坐标情形 设平面图形是由曲线 r = ϕ( ) θ 及射线θ = α ,θ = β 所围成的曲边扇形。 取极角θ 为积分变量,则 α ≤ θ ≤ β ,在平面图形中任意截取一典型的面积元 素ΔA,它是极角变化区间为[, ] θ θ + dθ 的窄曲边扇形。 ΔA的面积可近似地用半径为r = ϕ( ) θ , 中心角为dθ 的窄圆边扇形的面积来 代替,即 y = x y = −x 2 2 2 2 1 x y a b + = 2 2 2 2 1 x y b a + = x y O

A~deLoe[p(の)Pd从而得到了曲边梯形的面积元素dA=β1p(0)d0从而A=【例3】计算心脏线r=a(1+cos①)(a>O)所围成的图形面积。解:由于心脏线关于极轴对称,9021201.560150C1802103024030027020元12元1a?(1+cos0)2d0= a022cos2A=2Ide20200元122元408a2AO-de= 4a~Jcos4tdt「cos=t22003= 8a2 (4 - 1)!元.2一-a元224!!小结求在直角坐标系下、极坐标系下平面图形的面积。作业177
177 ΔA d ≈ 1 2 2 [ ( )] ϕθ θ 从而得到了曲边梯形的面积元素 dA d = 1 2 2 [ ( )] ϕθ θ 从而 A d = ∫ 1 2 2 ϕθθ α β ( ) 【例 3】计算心脏线r =+ > a a ( cos ) ( ) 1 0 θ 所围成的图形面积。 解: 由于心脏线关于极轴对称, A a da d a d a tdt a a t = + ∫ = ⎛ ⎝ ⎜ ⎞ ⎠ ∫ ⎟ = ∫ ∫ = − ⋅ = = 2 1 2 1 2 2 4 2 8 8 4 1 4 2 3 2 2 2 0 2 2 0 2 2 4 0 2 2 4 0 2 2 2 ( cos ) cos cos cos ( )!! !! θ θ θ θ θ θ π π π π π θ π 令 小结 求在直角坐标系下、极坐标系下平面图形的面积. 作业