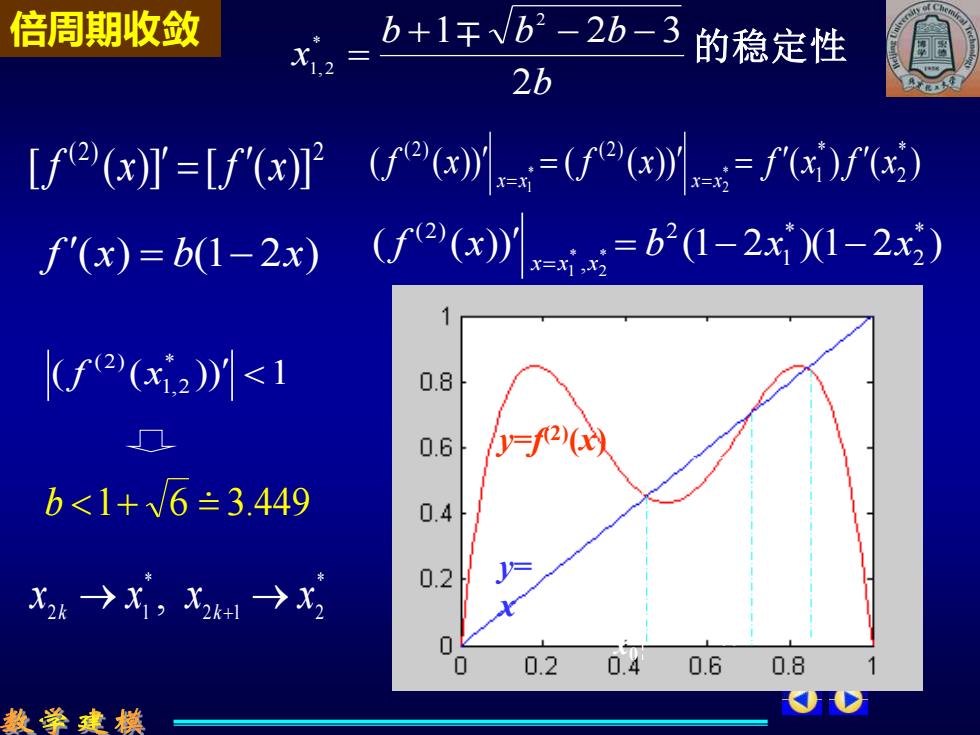
倍周期收敛 b+1千Vb2-2b-3 的稳定性 2b [(I=IOr Vfr) f'(x)=b(1-2x) (f2(x=5=b1-2x1-2x) (f2(xi2)川<1 0.8 口 0.6 =f2 b<1+√6=3.449 0.4 0.2 X2→X,X2H→X2 0 0.2 0.4 0.6 0.8 数学建模
( ( )) ( ( )) ( ) ( ) * 2 * 1 (2) (2) * 2 * 1 f x f x f x f x x x x x = = = = ( ( )) (1 2 )(1 2 ) * 2 * 1 2 , (2) * 2 * 1 f x b x x x x x = − − = ( ( )) 1 * 1,2 (2) f x 倍周期收敛 * 2 1 2 * 2 1 x x , x x k → k+ → b 1+ 6 = 3.449 f (x) = b(1− 2x) b b b b x 2 1 2 3 2 * 1,2 + − − = 的稳定性 (2) 2 [ f (x)] =[ f (x)] x1 * x2 * x * b=3.4 y=f (2)(x) y= x x0

倍周期收敛的进一步讨论 b>3.45→2(xi川>1x,x,(及x不稳定 出现4个收敛子序列x4kx4k+1,X4k+2,X4k+3 平衡点及其稳定性需研究X+4=f(x,) 3.449<b<3.544时有4个稳定平衡点4倍周期收敛 2n倍周期收敛,n=1,2,. bmc2n倍周期收敛的上界 b0=3,b1=3.449,b23.544,… n-→o,bm→3.57 >3.57,不存在任何收敛子序列 混沌现象 数学建模
倍周期收敛的进一步讨论 3.45 ( ( ))' 1 * 1,2 (2) b f x 出现4个收敛子序列 x4k , x4k+1 , x4k+2 , x4k+3 ( ) (4) k 4 k x = f x 平衡点及其稳定性需研究 + 3.449 b 3.544 时有4个稳定平衡点 2 n倍周期收敛, n=1,2,… bn~ 2n倍周期收敛的上界 b0=3, b1=3.449, b2=3.544, … n→, bn→3.57 x1 * , x2 * (及x * )不稳定 b>3.57, 不存在任何收敛子序列 混沌现象 4倍周期收敛