传染病模型(续) 数学建模·
传染病模型(续)

问题: 传染病模型 1。考虑人口出生率时如何? 2。考虑接触率、日治愈率随时间变化时如何? 数学建模 00
问题: 1。考虑人口出生率时如何? 2。考虑接触率、日治愈率随时间变化时如何? 传染病模型

模型5传染病有免疫性— 病人治愈 传染病模型 后即移出感染系统;传染病流 行期间,人口出生率为常数。 不考虑死亡、人口迁移。 假设 1)传染病流行期间,人口出生率为常数k 2)传染病流行期间,病人、健康人和移 出者的比例分别为i(t),s(t),r(t) 3)病人的日接触率入,日治愈率山, 接触数σ=2/4 数学建模
模型5 2)传染病流行期间,病人、健康人和移 出者的比例分别为 i(t),s(t),r(t) 3)病人的日接触率 , 日治愈率, 接触数 = / 假设 传染病有免疫性——病人治愈 后即移出感染系统;传染病流 行期间,人口出生率为常数。 不考虑死亡、人口迁移。 传染病模型 1)传染病流行期间,人口出生率为常数 k

模型4 传染病模型 di =入si-人ui di Asi-ui ds dt =-Asi+k ds =-见si+ r dt =人ui i(0)=o,s(0)=so i(0)=io,s(0)=so 数学建模
传染病模型 0 0 (0) , (0) di si i dt ds si k dt dr i dt i i s s = − = − + = = = 模型4 0 0 (0) , (0) di si i dt ds si k dt i i s s = − = − + = =
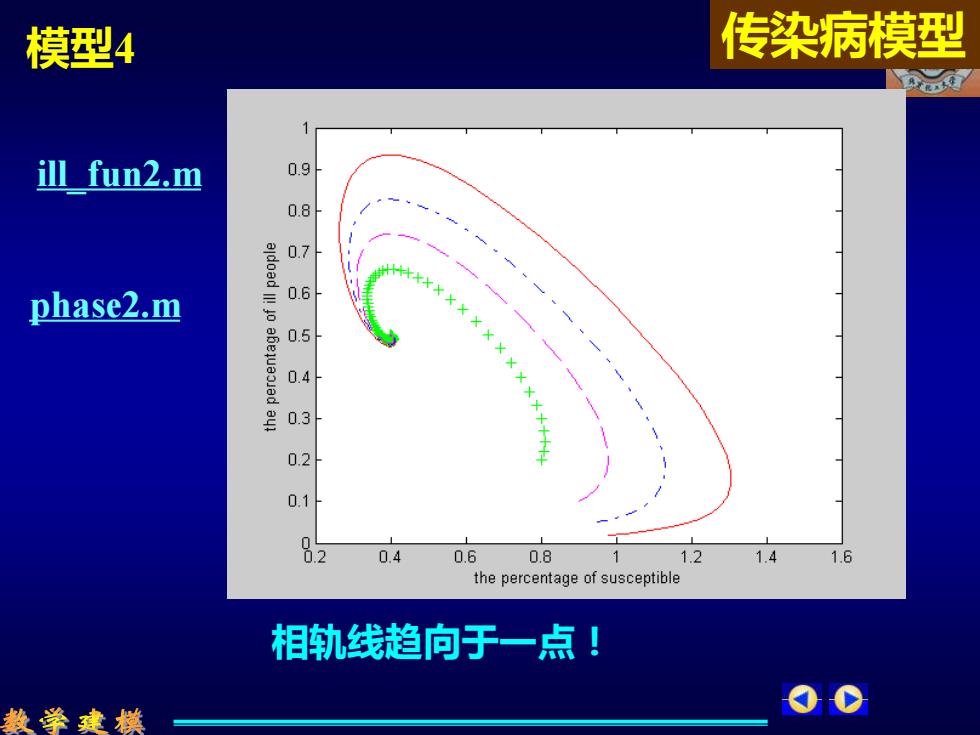
模型4 传染病模型 ill fun2.m 0.9 0.8 0.7 phase2.m 0.6 0.5 0.4 0.3 0.2 0.1 62 0.4 0.6 0.8 1.2 1.4 1.6 the percentage of susceptible 相轨线趋向于一点! 款学建模
模型4 传染病模型 相轨线趋向于一点! ill_fun2.m phase2.m