
Review ■散度: ● 设M是矢量场中的一点,在M的某个邻域内取 一包含M在内的任一闭合曲面,其所包含区域 的体积为△V,以△Φ表示穿出△s的通量。若 当该区域以任意方式缩向点M时, 明as 47 极限存在,则称之为矢量场在点M处的散度。 记为 H45 40 4=1 =lim AQMA △ lexu@mail.xidian.edu.cn
Review 散度: • 设M是矢量场中的 点一 ,在M的某个邻域内取 的某个邻域内取 一包含M在内的任一闭合曲面,其所包含区域 的体积为△V,以△φ表示穿出△s的通量。若 当该区域以任意方式缩向点M时, A ds 极限存在 则称之为矢量场在点M处的散度 V V s 极限存在,则称之为矢量场在点M处的散度。 记为 A ds lexu@mail.xidian.edu.cn 6 V V div A s M M lim lim
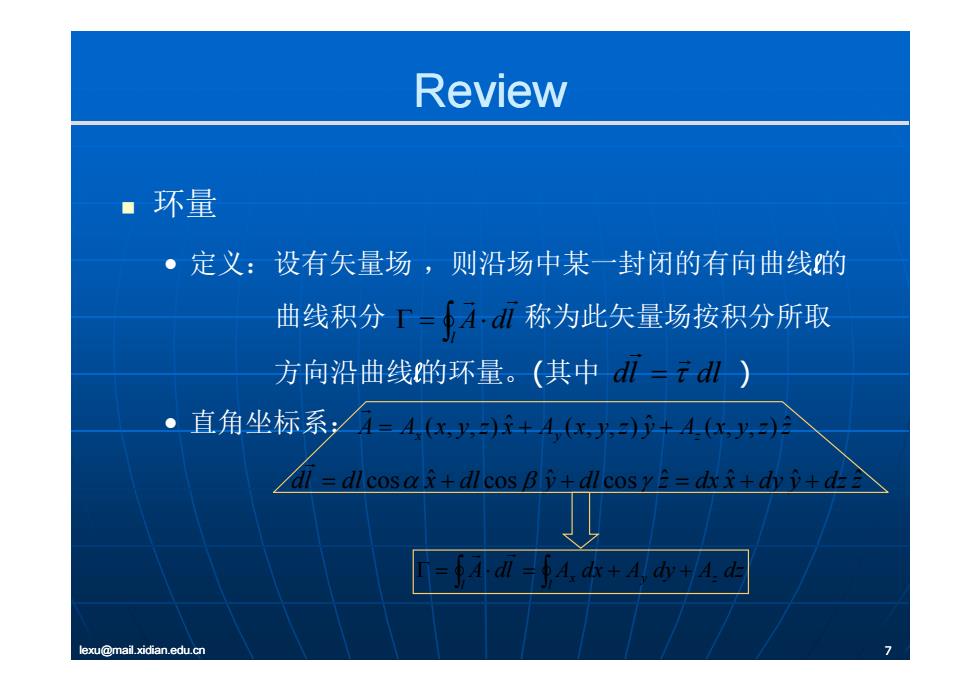
Review 。环量 。定义:设有矢量场,则沿场中某一封闭的有向曲线的 曲线积分「=4d称为此矢量场按积分所取 方向沿曲线的环量。(其中-dl-dl) 。直角坐标系4=4,+4,+4 =dl cos+dl cos B+l cosy6=d+d山)+北含 =4dl=4d本+4山+4 lexu@mail.xidian.edu.cn
Review 环量 • 定义:设有矢量场 ,则沿场中某 封闭的有向曲线 一封闭的有向曲线l的 曲线积分 称为此矢量场按积分所取 l A dl 方向沿曲线l的环量。(其中 ) • 直角坐标系: dl dl A A (x y z) xˆ A (x y z) yˆ A (x y z)zˆ • 直角坐标系:A A x y z x A x y z y A x y z z x y z ( , , ) ( , , ) ( , , ) dl dl x dl cos cos cos ˆ yˆ dl z dx x d ˆ ˆ ˆ y yˆ dz z l x y z l A dl A dx A dy A dz lexu@mail.xidian.edu.cn 7 l x y z l y
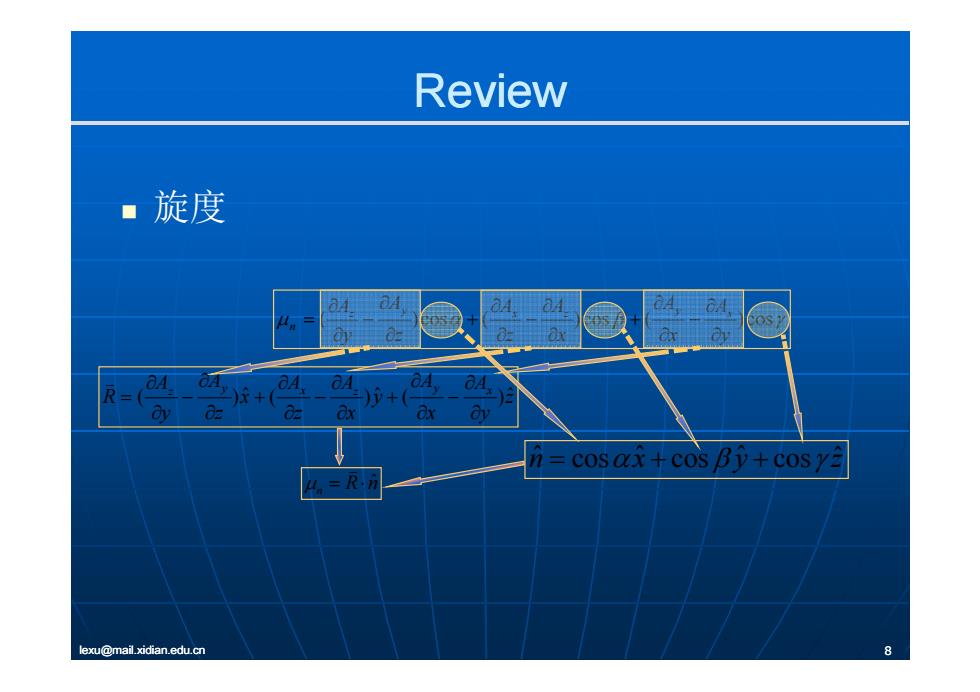
Review ■旋度 OS E n=cosax+cos By+cosy lexu@mail.xidian.edu.cn
Review 旋度 ( ) cos ( ) cos ( ) cos y A x A x A z A z A y Az y x z y x n z y A x A y x A z A x z A y A R z y x z y x ( )ˆ ( ) ˆ ( )ˆ n x yz ˆˆˆ cos cos cos ˆ ˆ n R n lexu@mail.xidian.edu.cn 8
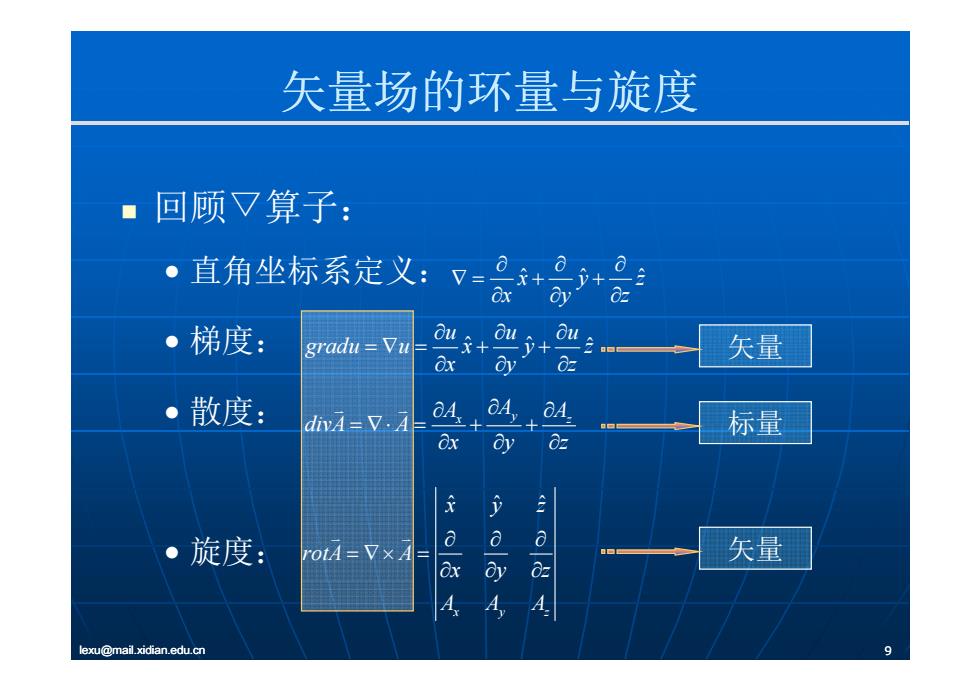
矢量场的环量与旋度 ■回顾又算子: ·直角坐标系定义: v=+0+0 。梯度: gradu Yu u+ 矢量 ·散度: dnA=又.A 6A. 标量 8x 0z 旋度: rotd Vx 4 xa pa 20论 矢量 A lexu@mail.xidian.edu.cn 9
矢量场的环量与旋度 回顾▽算子: • 直角坐标系定义: • 梯度: x y ˆ ˆ zˆ x y z ˆ ˆ ˆ uuu gradu u x y z • 梯度: 矢量 • 散度: gradu u x y z x y z x y z A A A divA A 矢量 标量 xyz ˆ ˆ ˆ 散度 divA A x y z 标量 xyz rotA A x y z • 旋度: 矢量 lexu@mail.xidian.edu.cn 9 x y z y A A A

矢量场的环量与旋度 ·旋度运算法则 1°VX(c)=cVxA(c-常数) 5°VxWw)=0 2°Vx(d±历=7x4士7x8 6°V.x方=0 3°7x(i=w7x+7wxa 7°vx7x1-W方-7a 4°V(dx)=o1.B-mti 其中V称为拉普拉斯算子,在直角坐标系中有 V2=77= a2,a2,∂2 h=0头+必品 2z2 +a V2a=2A+V249+242 lexu@mail.xidian.edu.cn 10
矢量场的环量与旋度 • 旋度运算法则 lexu@mail.xidian.edu.cn 10