
xyd,其中D 是直线y=1, x=2,及例1计算ID所围的闭区域y=x1≤x≤2解:D为X-型区域D(1≤y≤xdxj xydy原式=2 x"[1xy?dx'[1x3-1x]dx8HIGH EDUCATION PRESS
例1 计算 ,其中D 是直线 y=1, x=2, 及 y=x 所围的闭区域. 解: D为X–型区域, 原式=
(x+)d,其中D由=x2和x=2围成计算例2D解:如图,D为X-型区域原式=(x+y)dydx10HIGH EDUCATION PRESS
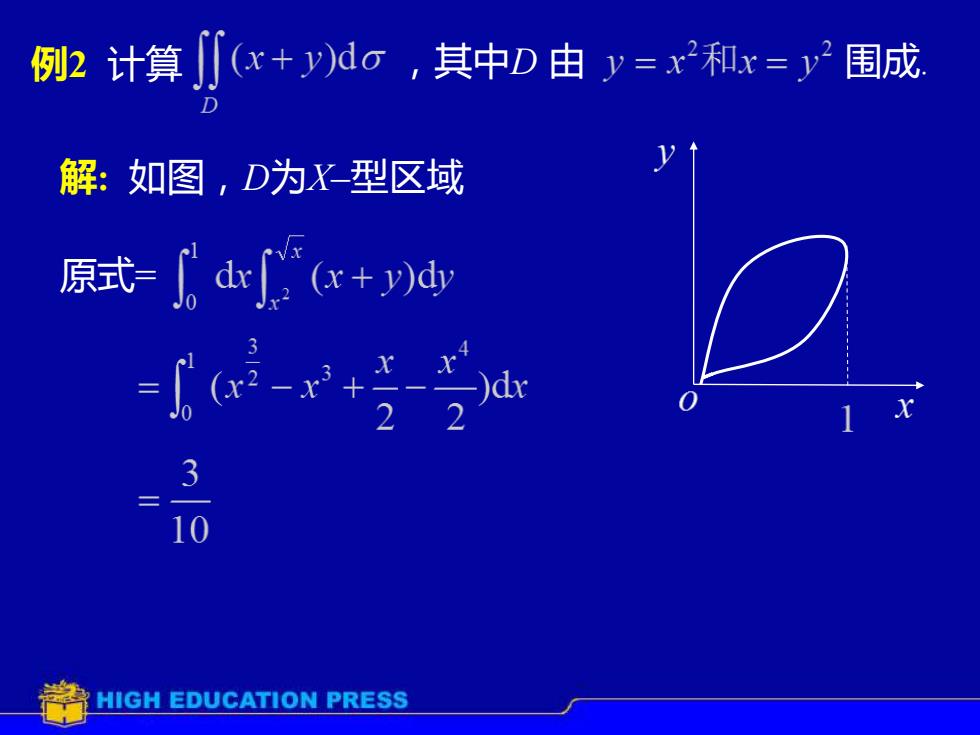
例2 计算 ,其中D 由 围成. 解: 如图,D为X–型区域 原式=

xyd,其中D 是抛物线2=x 及直线例3计算Dy=x-2 所围成的闭区域=x22中Dry=x-2HIGH EDUCATION PRESS
例3 计算 ,其中D 是抛物线 所围成的闭区域. 及直线

V)≤x≤y2()Y-型区域cdx=V2(y)x =Vi((y)Xf(x,y)do可化为二次定积分计算二重积分DW2(y)[ f(x,y)da=先x后yf(x, y)dxDHIGH EDUCATION PRESS机动上页下页返回结束自录
y d c o x ( ) 2 x = y ( ) 1 x = y 机动 目录 上页 下页 返回 结束 二重积分 可化为二次定积分计算: