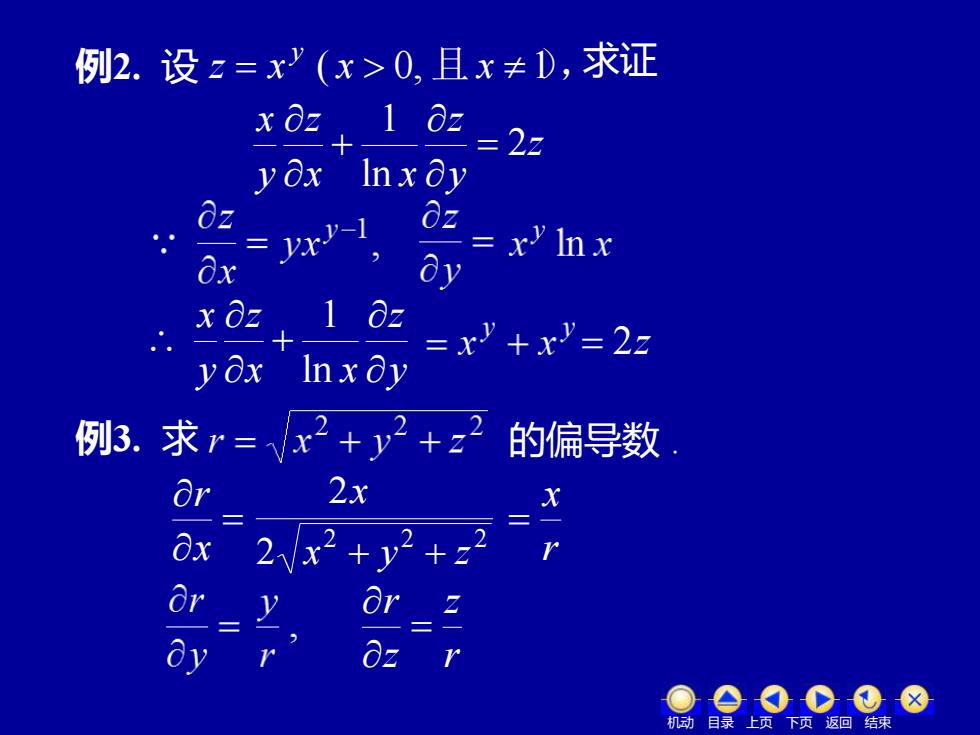
例2.设z=x'(x>0,且x≠D,求证 xOz 1 0z 0=22 yOx 0z =yxy-1 0 8x 2=x"Inx O x0z,1 Oz yOx Inxay =x'+x'=2 例3. 求r=x2+y2+z2 的偏导数 2x = Ox 2x+ 2+ Or r dy 0z 下页返回结束
例2. 设 z = x y ( x 0, 且 x 1), z y z x x z y x 2 ln 1 = + 证: y z x x z y x + ln 1 例3. 求 的偏导数 . 解: = x r 求证 = 2z 2 2 2 2 x + y + z 2x r x = r z z r = 机动 目录 上页 下页 返回 结束

例4.已知理想气体的状态方程pV=RTR为常数) 求证 op av ar =-1 RT RT 说明: V= RT R 偏导数记号是一个 p aT p 整体记号,不能看作 T- pV ol V 分子与分母的商! R R op av RT =-1 av ol op 机动目录上页下页返回结束
偏导数记号是一个 例4. 已知理想气体的状态方程 求证: = −1 p T T V V p 证: , V RT p = , p RT V = = p T T V V p 说明: (R 为常数) , = V p 2 V RT − = T V p R pV RT − = −1 不能看作 分子与分母的商 ! 此例表明, 机动 目录 上页 下页 返回 结束 整体记号

2.二元函数偏导数的几何意义: ds,0)m y=y。 是曲线 任在点场处的 y=Yo MT,对x轴的斜率 0 y=Yo }y-x 是曲线 2=/(,》在点M处的切线MoT,对y轴的 X=X0 斜率 HIGH EDUCATION PRESS 机动目 下页返回结束
2.二元函数偏导数的几何意义: 0 0 ( , ) d d 0 0 x x f x y x x f x x y y = = = = = = 0 ( , ) y y z f x y M0Tx 0 0 ( , ) d d 0 0 y y f x y y y f x x y y = = = = 是曲线 M0Ty 在点 M0 处的切线 对 x 轴的斜率. 在点M0 处的切线 斜率. 是曲线 y x z 0 x Ty o Tx 0 y M 0 机动 目录 上页 下页 返回 结束 对 y 轴的
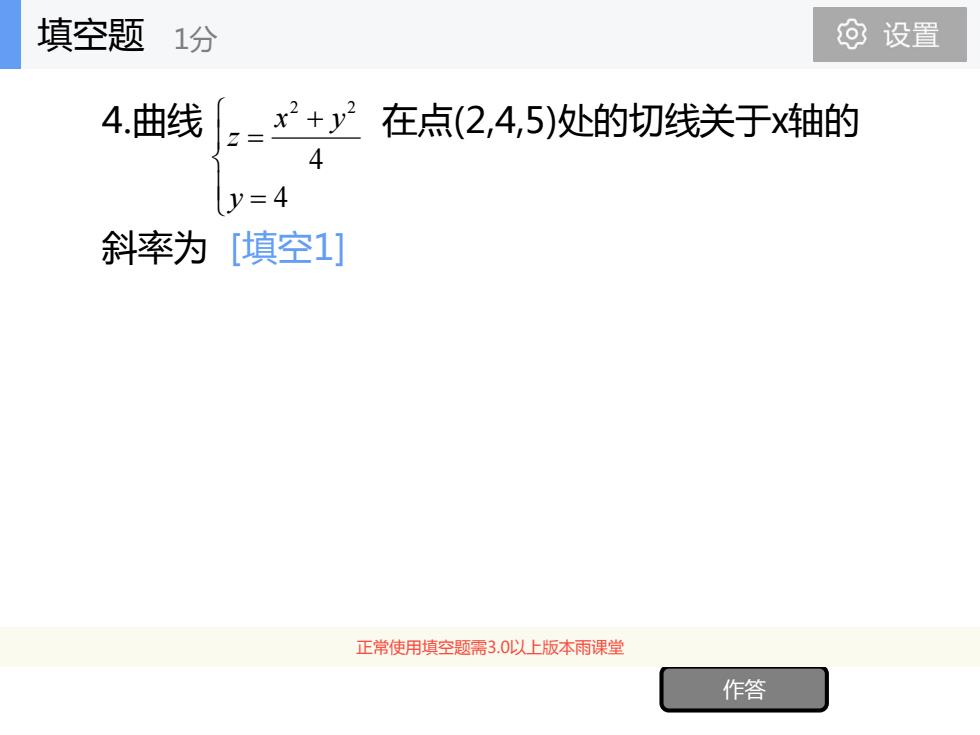
填空题1分 设置 4.曲线-x2+y2 在点(2,4,5)处的切线关于轴的 4 y=4 斜率为[填空1] 正常使用填空题需3.0以上版本雨课堂 作答
4.曲线 在点(2,4,5)处的切线关于x轴的 斜率为 [填空1] 作答 正常使用填空题需3.0以上版本雨课堂 = + = 4 4 2 2 y x y z 填空题 1分

注意:函数在某点各偏导数都存在 但在该点不一定连续 例如,2=f(x,)={x x2+y2≠0 +y ,x2+y2=0 显然 k0,0=fx x=0=0 J,0.)=f0 y=0=0 在上节已证f(x,y)在点(0,0)并不连续! HIGH EDUCATION PRESS 上节例目录上页下页返回结束
函数在某点各偏导数都存在, 显然 例如, + = + = = + 0 , 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy z f x y = 0 = 0 注意: 但在该点不一定连续. 上节例 目录 上页 下页 返回 结束 在上节已证 f (x , y) 在点(0 , 0)并不连续!