
同样可定义对y的偏导数 f(xo.)lim f(xo.+)-f(xo-yo) △y>0 △y -jy fGay-n 若函数z=f(x,y)在域D内每一点(x,y)处对x 或y偏导数存在,则该偏导数称为偏导函数,也简称为 偏导数,记为 6z Of Ox'Ox ,x,Jx),x az of ay' Oy ,f,x HIGH EDUCATION PRESS 机动目录上页下页返回结束
同样可定义对 y 的偏导数 lim →0 = y ( , ) 0 0 f x y y 若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 则该偏导数称为偏导函数, 也简称为 偏导数 , ( , ) , ( , ) 2 f x y f x y y ( , ) 0 f x ( , ) 0 − f x y 记为 y + y 0 0 y 机动 目录 上页 下页 返回 结束 或 y 偏导数存在 , , , , y z y f y z

偏导数的概念可以推广到二元以上的函数 例如,三元函数u=f(x,y,)在点(x,y,)处对x的 偏导数定义为 厂(x,yz))=1im/x+Ax,2)-fx,y,) △x→0 △x f(xy,)=? (请自己写出) f(x,y,)=? HIGH EDUCATION PRESS 机动目录上页下页返回结束
例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 偏导数的概念可以推广到二元以上的函数 . x x + x f (x, y,z) = ? y f (x, y,z) = ? z x 机动 目录 上页 下页 返回 结束 偏导数定义为 (请自己写出)
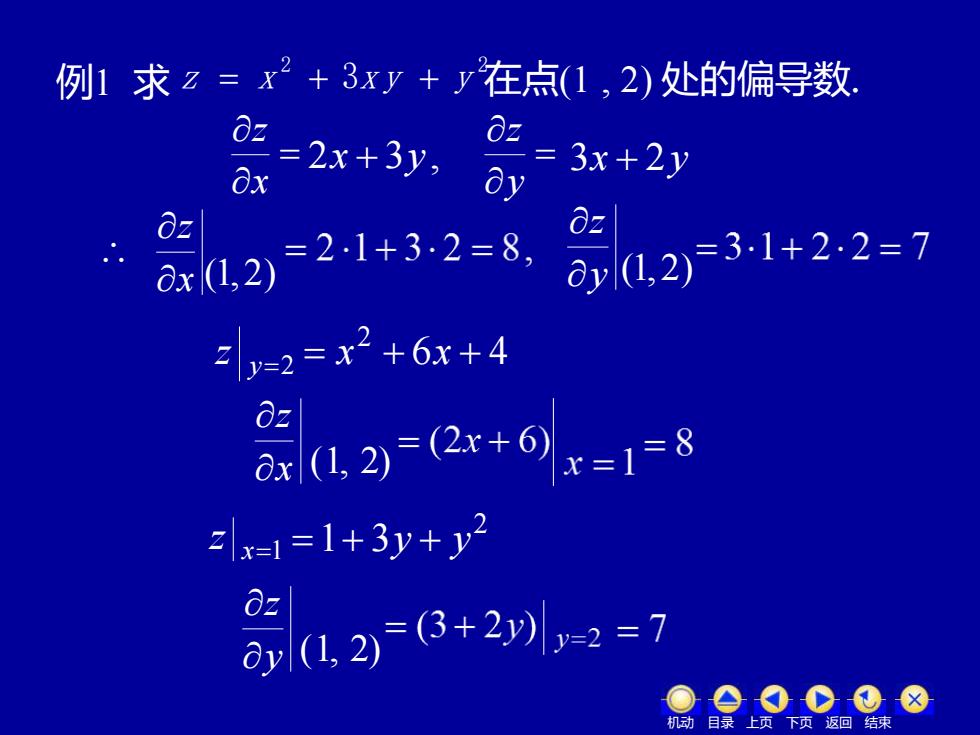
例1求2=x2+3xy+y在点(1,2)处的偏导数 2+3y2 x 2321-32=8 0z 12)31+22=7 2=2=x2+6x+4 03-2+01 x=1=1+3y+y 器262=7 机动目录上页下页返回结束
例1 . 求 2 2 z = x + 3x y + y 解法1: = x z x (1,2) z 解法2: x (1, 2) z 在点(1 , 2) 处的偏导数. y (1, 2) z 2x + 3y , = y z 3x + 2y y (1,2) z 6 4 2 = x + x + x=1 z 2 =1+ 3y + y y=2 z 机动 目录 上页 下页 返回 结束 例1 求
单选题1分 ⊙设置 2.设z=xsiny ,则 2 525 -2 HIGH EDUCATION PRESS 提交
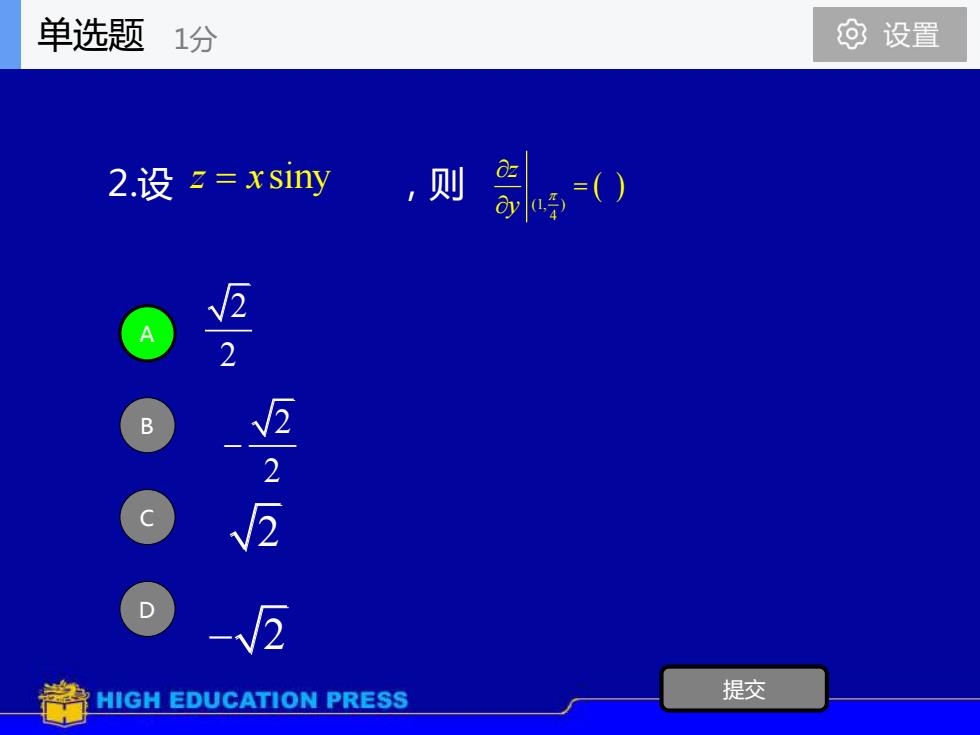
2.设 ,则 A B C D 提交 z x = siny ( ) (1, ) 4 z y = 2 2 2 2 − 2 − 2 单选题 1分

单选题 2分 ⊙设置 3.设 x-y 则 年(0)0 -2y 2x x-y)2’(x-)7 B 2y 2x (x-y)2'(x-y)2 -2y -2x (x-y)2(x-y)7 2y -2x (x-y)2’(x-y)2 提交
3.设 则 A B C D 提交 x y z x y + = − ( ), ( ) z z x y = = 2 2 2 2 , ( ) ( ) y x x y x y − − − 2 2 2 2 , ( ) ( ) y x x y x y − − 2 2 2 2 , ( ) ( ) y x x y x y − − − − 2 2 2 2 , ( ) ( ) y x x y x y − − − 单选题 2分