
§3.2搜索区间的确定 常用的一维直接法有消去法和近似法两类。它们都是从 某个初始搜索区间出发,利用单峰函数的消去性质,逐步缩 小搜索区间,直到满足精度要求为止。 §3.2.1单峰函数 定义:如果函数fx)在区间[a,b]上只有一个极值点,则称fx)为 [a,b上的单峰函数。 fx)↑ f(x) a 连续单峰函数 非单峰函数
f(x) a b x §3.2 搜索区间的确定 常用的一维直接法有消去法和近似法两类。它们都是从 某个初始搜索区间出发,利用单峰函数的消去性质,逐步缩 小搜索区间,直到满足精度要求为止。 §3.2.1 单峰函数 连续单峰函数 f(x) a b x 不连续单峰函数 f(x) x a b 离散单峰函数 f(x) a b x 非单峰函数 定义:如果函数f(x)在区间[a,b]上只有一个极值点, 则称f(x)为 [a, b]上的单峰函数
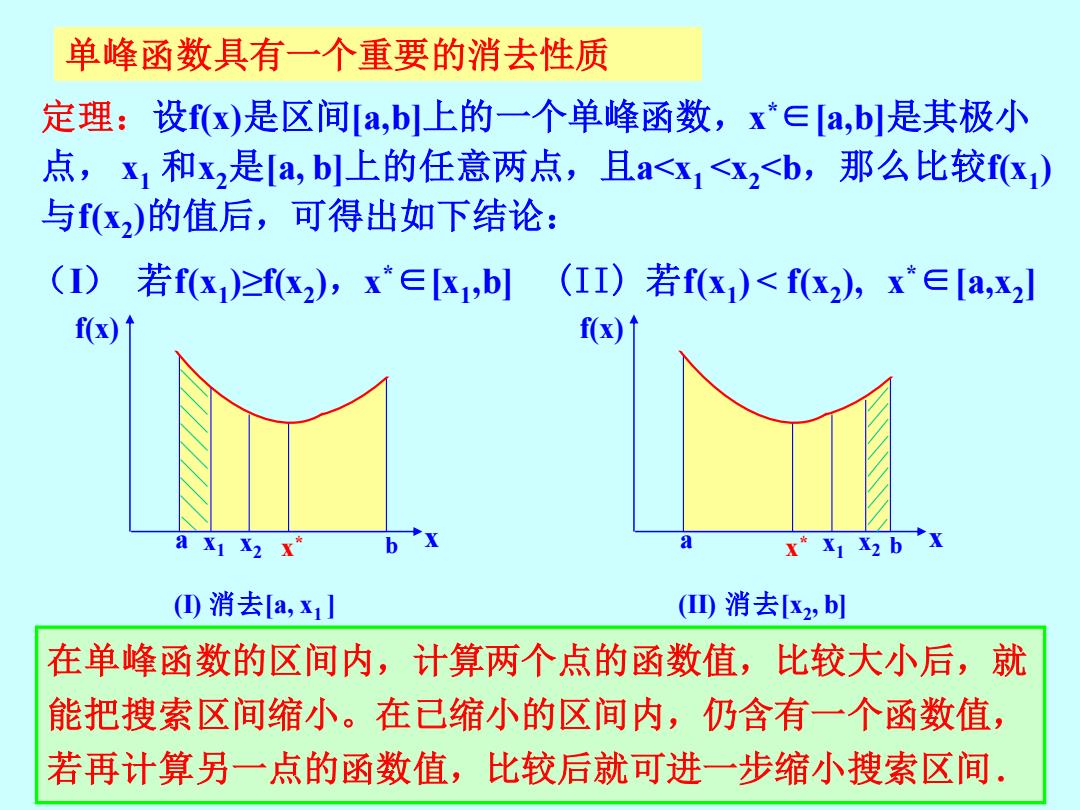
单峰函数具有一个重要的消去性质 定理:设fx)是区间a,b上的一个单峰函数,x*∈[a,b是其极小 点,x1和x,是[a,b上的任意两点,且a<x1<x2<b,那么比较飞) 与x)的值后,可得出如下结论: (I) 若fx1)≥fk2),x*∈K1,b] (II)若fx)<fx2),x*∈[a,x2l f(x) f(x) a x X2 x" (①消去a,x1】 (四消去[K2,b 在单峰函数的区间内,计算两个点的函数值,比较大小后,就 能把搜索区间缩小。在已缩小的区间内,仍含有一个函数值, 若再计算另一点的函数值,比较后就可进一步缩小搜索区间
单峰函数具有一个重要的消去性质 定理:设f(x)是区间[a,b]上的一个单峰函数,x *∈[a,b]是其极小 点, x1 和x2是[a, b]上的任意两点,且a<x1 <x2<b,那么比较f(x1 ) 与f(x2 )的值后,可得出如下结论: f(x) a b x (I) 消去[a, x1 ] x x * 1 x2 f(x) a b x (II) 消去[x2 , b] x * x1 x2 (II) 若f(x1 ) < f(x2 ), x*∈[a,x2 ] 在单峰函数的区间内,计算两个点的函数值,比较大小后,就 能把搜索区间缩小。在已缩小的区间内,仍含有一个函数值, 若再计算另一点的函数值,比较后就可进一步缩小搜索区间. (I) 若f(x1 )≥f(x2 ),x *∈[x1 ,b]
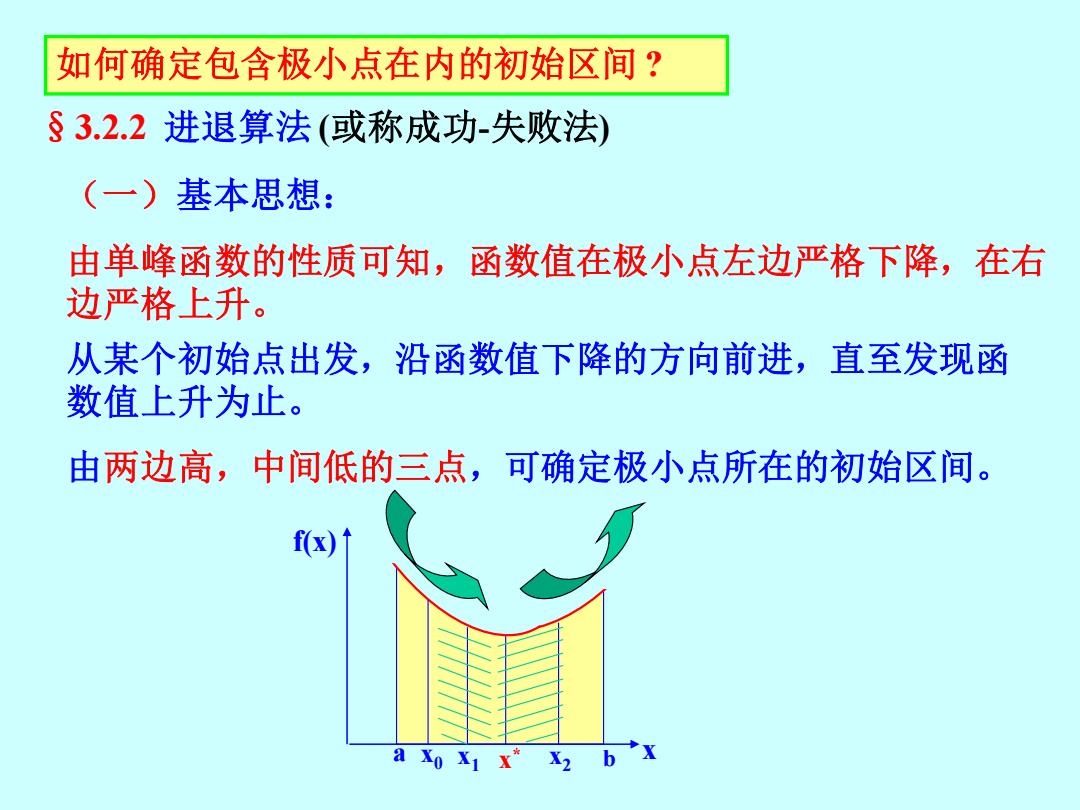
如何确定包含极小点在内的初始区间? §3.2.2进退算法(或称成功-失败法) (一)基本思想: 由单峰函数的性质可知,函数值在极小点左边严格下降,在右 边严格上升。 从某个初始点出发,沿函数值下降的方向前进,直至发现函 数值上升为止。 由两边高,中间低的三点,可确定极小点所在的初始区间。 f(x) a xo x1 x*X2 bx
§3.2.2 进退算法 (或称成功-失败法) 如何确定包含极小点在内的初始区间 ? (一)基本思想: 由单峰函数的性质可知,函数值在极小点左边严格下降,在右 边严格上升。 f(x) a b x x x * 0 x1 x2 从某个初始点出发,沿函数值下降的方向前进,直至发现函 数值上升为止。 由两边高,中间低的三点,可确定极小点所在的初始区间
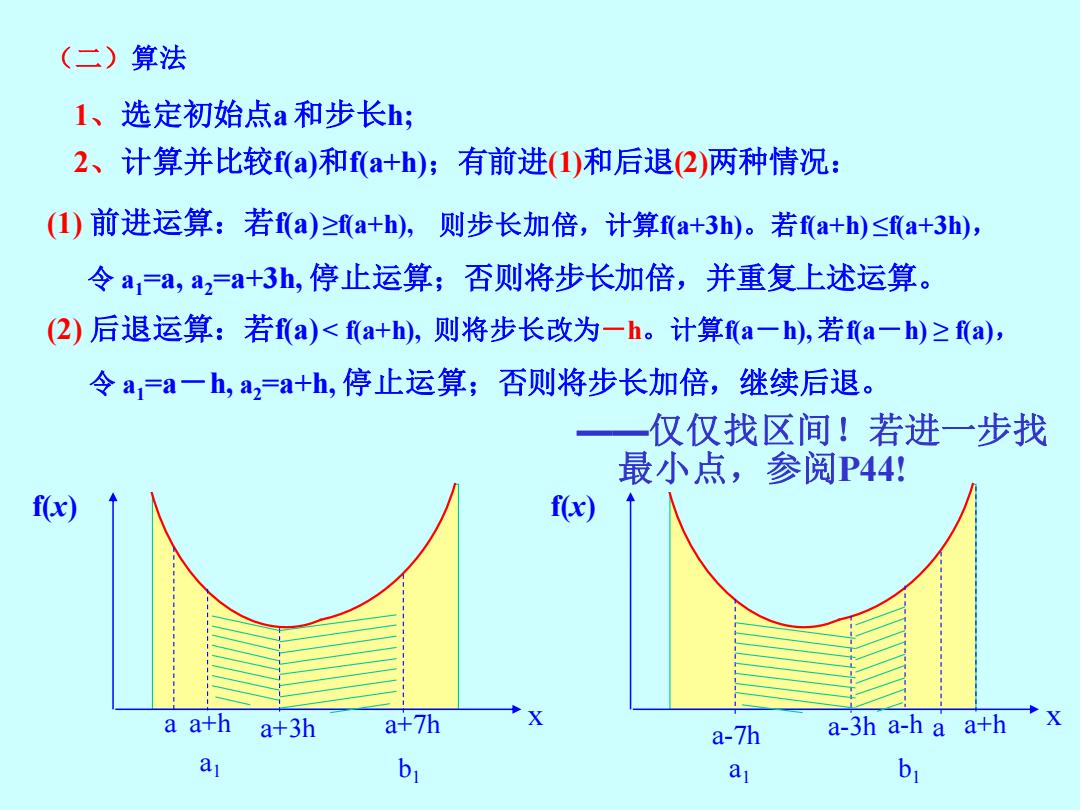
(二)算法 1、选定初始点a和步长h; 2、计算并比较f(a)和f(a+h);有前进(1)和后退(2)两种情况: ()前进运算:若fa)≥fa+h),则步长加倍,计算fa+3h)。若fa+h)≤fa+3h), 令a=a,a2=a+3h,停止运算;否则将步长加倍,并重复上述运算。 (2)后退运算:若fa)<fa+h),则将步长改为一h。计算fa一h),若fa一h)≥fa), 令a1=a一h,a2=a+h,停止运算;否则将步长加倍,继续后退。 一仅仅找区间!若进一步找 最小点,参阅P44! f(x) f(x) a ath a+3h a+7h X a-3h a-h aa+h X a-7h a b1 a
(二)算法 1、选定初始点a 和步长h; f(x) x 2、计算并比较f(a)和f(a+h);有前进(1)和后退(2)两种情况: (1) 前进运算:若f(a) ≥f(a+h), (2) 后退运算:若f(a) < f(a+h), a a+h 则步长加倍,计算f(a+3h)。若f(a+h) ≤f(a+3h), 令 a1=a, a2=a+3h, 停止运算;否则将步长加倍,并重复上述运算。 a+3h f(x) x a+7h a a+h a1 b1 a-3h a-h a-7h a1 b1 则将步长改为-h。计算f(a-h), 若f(a-h) ≥ f(a), 令 a1=a-h, a2=a+h, 停止运算;否则将步长加倍,继续后退。 ——仅仅找区间!若进一步找 最小点,参阅P44!

(三)几点说明 缺点:效率低; 优点:可以求搜索区间; 注意:选择要适当,初始步长不能选得太小;
(三) 几点说明 缺点:效率低; 优点:可以求搜索区间; 注意:h选择要适当,初始步长不能选得太小;