
2.实用收敛性(续) ▲收敛性:设解集S*≠◆,{x为算法产生的点 列。下列情况之一成立时,称算法收敛: 1°3xk)∈S*; ←有限步终止 2°x)图*,Vk,{xk的任意极限点x*∈S*。 ▲全局收敛:对任意初始点x,算法均收敛。 局部收敛:当x山)充分接近解x*时,算法收敛
2.实用收敛性(续) ▲收敛性:设解集S*≠ ,{x (k) }为算法产生的点 列。下列情况之一成立时,称算法收敛: 1°x (k) ∈S*; 2° x (k) S* , k,{x (k) }的任意极限点x* ∈S* 。 ▲全局收敛:对任意初始点x (1) ,算法均收敛。 局部收敛:当x (1) 充分接近解x*时,算法收敛。 有限步终止

三、收敛速度 设算法产生点列x收敛到解x*,且xkx*,Vk, 关于算法的收敛速度,有 1线性收敛: x+”-x儿<1当充分大时成立。 llxll 2.超线性收敛: lim ‖x-x‖=0 lx)-x"ll 3.二阶收敛:3a>0,是使当充分大时有 llD-x*l ≤d llx-x"112
三、收敛速度 设算法产生点列{x (k) } 收敛到解x*,且x (k)≠x*, k, 关于算法的收敛速度,有 1.线性收敛: 当k充分大时成立。 2.超线性收敛: 3.二阶收敛: ﹥0,是 使当k充分大时有 0 || || || || lim ( ) * ( 1) * = − − + → x x x x k k k − − + ( ) * 2 ( 1) * || || || || x x x x k k 1 || || || || ( ) * ( 1) * − − + x x x x k k

三、收敛速度(续) 定理:设算法点列x超线性收敛于x*,且xx*, Vk,那么 lim 【x+-xⅡ=1 k→ lxk)-x*Ⅱ 证明:只需注意 1+)-x‖-lxW-x*‖1≤x+)-xW‖≤lx+)-x0 +x-x*‖,除财x因-x*‖并令北→oo,利用超线 性收敛定义可得结果。 该结论导出算法的停止条件可用: Ixk+)-xIKε或1f(x+)-f(x)K6
三、收敛速度(续) 定理:设算法点列{x (k) }超线性收敛于x*,且x (k)≠x* , k,那么 证明:只需注意 | ||x(k+1) –x * || -|| x(k) –x* || |≤ ||x(k+1) –x (k) || ≤ ||x(k+1) –x * || +|| x(k) –x* || ,除以|| x(k) –x* || 并令k→∞,利用超线 性收敛定义可得结果。 1 || || || || lim ( ) * ( 1) = − − + → x x x x k k (k) k 该结论导出算法的停止条件可用: ( ) 1 ( ) || || k k x x + − ( ) 1 ( ) | ( ) ( ) | k k f x f x + 或 −

四、二次终结性 ▲一个算法用于解正定二次函数的无约束极小 时,有限步迭代可达最优解,则称该算法具 有二次终结性
四、二次终结性 ▲一个算法用于解正定二次函数的无约束极小 时,有限步迭代可达最优解,则称该算法具 有二次终结性
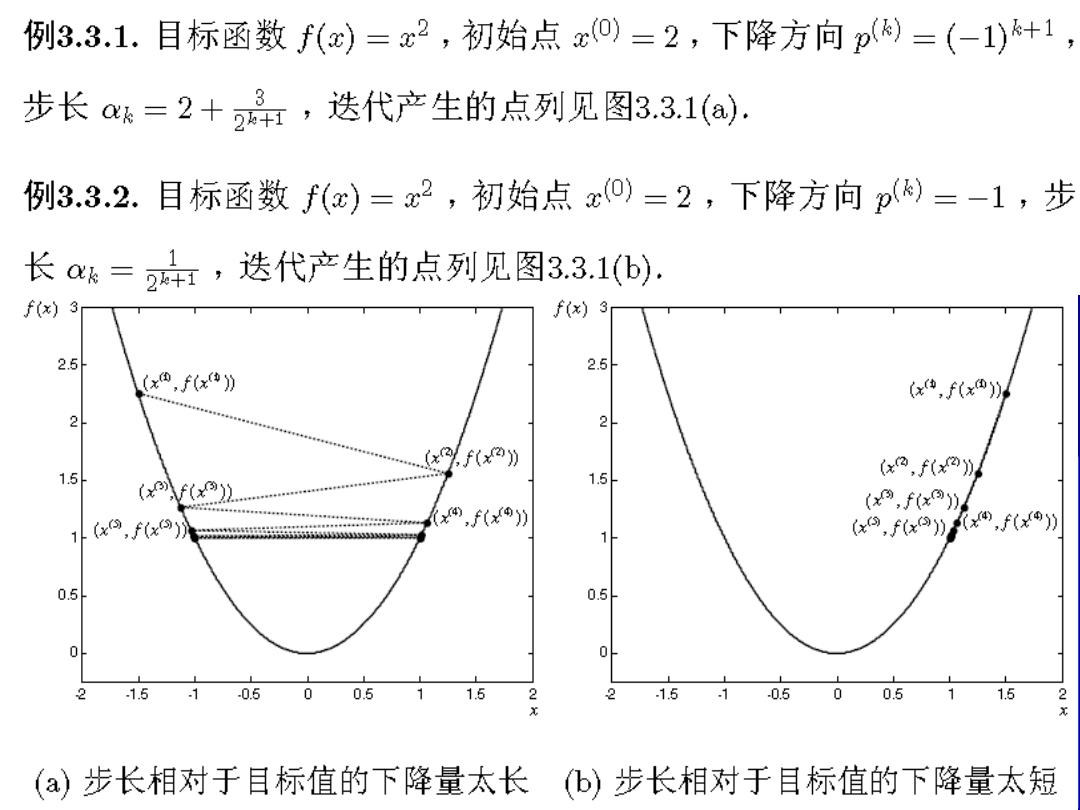
例3.3.1.目标函数f(c)=x2,初始点xo)=2,下降方向p()=(-1)+1 步长k=2+2,迭代产生的点列见图33.1(a. 例3.3.2.目标函数f()=2,初始点xo)=2,下降方向p()=-1,步 长=24,迭代产生的点列见图3.3.1(b). f(x)3 f(x)3 2.5 2.5 (x④,fx》 (x,fx®)4 2 2 (xf() 1.5 1.5 (x,fx》 (,f(x) (.f(x) 1(x,fx) x9,f)(,f) 0.5 0.5 01 2 -1.5 1 -0.5 0 0.5 1.5 2 2 1.5 .1 0.5 0 0.5 1.5 2 (a)步长相对于目标值的下降量太长 (b)步长相对于目标值的下降量太短