
第八章向量代数与空间解析几何1112.试用向量证明不等式:Vai+a+abi+b+b≥ab+ab2+abl其中a1,a2,a3,b1,b2.b,为任意实数.并指出等号成立的条件证设向量a=(ai,a2.a),b=(bi,b2.b,).由a.b=[a|/b|cos(a,b)知,la.b|=|alb|lcos(a,b)|≤|alb|,从而lab,+a2b2+a3b3l≤ai+a3+a3b+b2+b3当41,42,43与b1,b2,b3成比例,即%-%2-时,上述等式成立,bb2b3习题8平面及其方程1.求过点(30,-1)且与平面3x-7y+5z-12=0平行的平面方程解所求平面与已知平面3x-7y+5z-12=0平行.因此所求平面的法向量可取为n=(3,-7,5),设所求平面为3x-7y+5z+D=0.将点(3,0,-1)代入上式得D=-4.故所求平面方程为3x-7y+5z=4=02.求过点M。(2,9,-6)且与连接坐标原点及点M。的线段0M。垂直的平面方程解OM。=(2,9,-6).所求平面与OM。垂直,可取n=0M。,设所求平面方程为2x+9y-6z+D=0.将点M。(2,9,-6)代人上式,得D=-121.故所求平面方程为2x+9y-6z-121=0.23.求过(1,1,-1),(-2,-2,2)和(1,-1,2)三点的平面方程y-1 z+1x-1=0,得x-3y-2z=0,即为所求平面方程解由-21-2-12+12+11-1-1-1注设M(x,y,z)为平面上任一点,M(x,yi,z)(i=1,2,3)为平面上已知点由MM.(MM,×MM)=0,印2-21X-XIy-yI=0,22-21X2-X1y2-yI3-21X-xY3-Y1它就表示过已知三点M(i=1,2,3)的平面方程4.指出下列各平面的特殊位置,并画出各平面:(2)3y-1=0;(1)x=0;
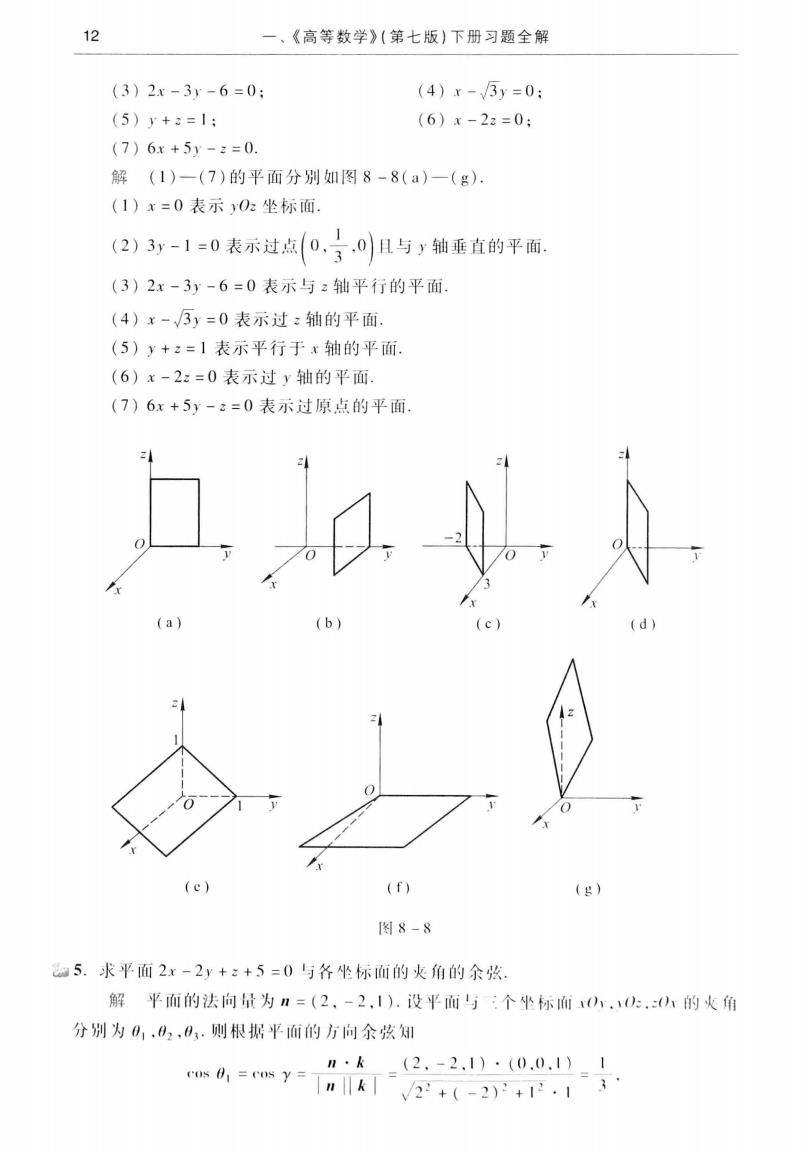
12、《高等数学》(第七版)下册习题全解(4)x-/3y=0:(3)2x-3y-6=0;(5) y+s=l:(6)x-22=0:(7)6x+5y=z=0解(1)一(7)的平面分别如图8-8(a)一(g).(1)x=0表示y0z坐标面(2)3y-1=0表示过点(0.0)且与轴垂直的平面(3)2x-3y-6=0表示与z轴平行的平面,(4)x-/3y=0表示过:轴的平面(5)y+z=1表示平行于x轴的平面(6)x-2z=0表示过轴的平面(7)6x+5y-z=0表示过原点的平面二4(a)(b)(c)(d)240-0(e)(f)(g)图8-85.求平面2x-2y+z+5=0与各坐标面的火角的余弦解平面的法向量为n=(2,-2.1).设平面与个坐标面0.0.0的火角分别为0,.62.0.则根据平面的方向余弦知n·k(2.-2.1).(0.0.1)1coso,=cosV22+(-2)+.1"3nllk

第八章向量代数与空间解析几何13n.i(2,-2,1):(1,0,0)2cos,=cosα3[n][i]3.1-(2,-2,1) ·(0,1,0)-2n.jcos6,=cosβ3nlli3.16.一平面过点(1.0,-1)且平行于向量a=(2,11)和b=(1,-1,0),试求这平面方程.解所求平面平行于向量a和b,可取平面的法向量[ikj211n=axb=1=(1,1,-3),1101故所求平面为1:(x-1)+1·(y-0)-3·(z+1)=0即x+y-3z-4=07.求三平面x+3y+z=1,2x-y-2=0,-x+2y+2z=3的交点解联立三平面方程x+3y+z=1,2x-y-z=0,-x+2y+2z=3.解此方程组得x=1,y=-1,z=3.故所求交点为(1,-1,3).8.分别按下列条件求平面方程:(1)平行于x0z面且经过点(2,-5,3);(2)通过z轴和点(-3,1,-2);(3)平行于x轴且经过两点(4,0,-2)和(5,1,7)解(1)所求平面平行于xOz面,故设所求平面方程为By+D=0.将点(2,-5,3)代人,得-5B+D=0,即D=5B.因此,所求平面方程为即y+5=0By+5B=0,(2)所求平面过z轴,故设所求平面方程为Ax+By=0.将点(-3,1,-2)代人,得即B=3A.-3A+B=0.因此,所求平面方程为Jx+3y=0即Ax+3Ay=0,(3)所求平面平行于x轴,故设所求平面方程为By+Cz+D=0.将点(4,0,-2)及(51,7)分别代人方程得B+7C+D=0及-2C+D=09Dc=:-DB=从而解得2

14一、《高等数学》(第七版)下册习题全解因此,所求平面方程为9DZ+D=0.Dy+22即9y-z-2=09.求点(1.2,1)到平面x+2y+2z-10=0的距离解利用点Mo(xo,Yo,Zo)到平面Ax+By+Cz+D=0的距离公式IAxo +Byo+Czo +Dd-A2+ B2+ C21+2.2+2.1-10[ - 3]13V12+22+22习题8空间直线及其方程1.求过点(4,-1,3)且平行于直线=3的直线方程215解所求直线与已知直线平行,故所求直线的方向向量s=(2.1,5).直线方程即为x-4y+lz-32512.求过两点M,3,-2,1)和M,(-1,02)的直线方程解取所求直线的方向向量S=M,M,=(-1-3,0-(-2),2-1)=(-4.2,1).因此所求直线方程为x-3_y+2 z-1-4213.用对称式方程及参数方程表示直线x-y+z=l.[2x+y+z=4.解根据题意可知已知直线的方向向量iIk1-1-S==(-2.1.3)21135取x=0,代人直线方程得解得!这样就得到直线经过71Ly+2=4.35的一点0,因此直线的对称式方程为22

第八章向量代数与空间解析几何1535-y2x-02-213参数方程为-2t,3+1C5+31.2注由于所取的直线上的点可以不同,因此所得到的直线对称式方程或参数方程的表达式也可以是不同的。4.求过点(2.0,-3)且与直线[x-2y+4z-7=0,3x+5y-2z+1=0垂直的平面方程根据题意,所求平面的法向量可取已知直线的方向向量,即解[ikj-241=(-16,14,11),n=s=35-2故所求平面方程为-16(x-2)+14(y-0)+11(z+3)=0.即16x-14y-11z-65=0[2x+2y-z+23=05x-3y+3z-9=05.求直线的夹角的余弦与直线[3x+8y+z-18=0[3x-2y+z-1=0解两已知直线的方向向量分别为kk[ijij232-1=(10,-5,10),53=(3.4.-1).S2=S,=381-213因此,两直线的夹角的余弦S,:S2cos 6 = cos(S,,S2)s,//s2/3×10-4×5-1×10=0/32+42+(-1)2/102+(-5)2+102[3x+6y-3z=8,[x+2y-z=7,平行6.证明直线与直线[2x-y-z=02x+y+z=7已知直线的方向向量分别是证